Найдем сумму первых натуральных чисел по формуле сумме первых членов арифметической прогрессии:
Рассмотрим числитель дроби: - произведение двух подряд идущих натуральных чисел, значит одно из них четное, а другое нечетное. Если четное число делится только на 2, но не делится на 4, то при вычислении значения дроби множитель "2" сократится и получившийся результат будет нечетным. Если четное число делится хотя бы на 4, то при вычислении значения дроби один множитель "2" сократится, но еще как минимум один множитель "2" останется и результат будет четным.
Итак, для четного результата сложения необходимо, чтобы хотя бы один из множителей произведения делился на 4.
1 случай: делится на 4 (или же можно сказать, что при делении на 4 дает остаток 0).
2 случай: делится на 4, тогда при делении на 4 дает остаток 3.
Если эти условия не выполняются, то результат сложения будет нечетным. То есть, можно сказать, что это происходит, когда при делении на 4 дает остаток 1 или 2.
ответ: четный результат - когда при делении на 4 дает в остатке 0 или 3; нечетный результат - когда при делении на 4 дает в остатке 1 или 2.
первые n натуральных чисел - это арифметическая прогрессия с разностью равной 1 и таким же первым членом, тогда по формуле сумма первых n ее членов равна: ((n+1)*n)/2, эту формулу можно преобразовать следующим образом: n * (n+1)/2, для нечетного n и (n+1) * n/2, для четного n. В первом случае результат зависит от (n+1)/2, каким оно будет по четности, таким и будет результат, аналогично во втором случае все зависит от n/2. Нетрудно заметить, что и n/2 и (n+1)/2 чередуют свои четности с шагом 4, то есть если при n = 1 результат нечетный, то и при n = 5 результат тоже нечетный. Зная, что при n = 1 и n = 2 результаты нечетные, а при n = 3 и n = 4 четные, делаем вывод, что четность результата зависит от остатка при делении n на 4, а точнее, если остаток 1 или 2, то результат нечетный, а если 0 или 3, то четный.
Найдем сумму первых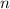 натуральных чисел по формуле сумме первых
натуральных чисел по формуле сумме первых 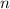 членов арифметической прогрессии:
членов арифметической прогрессии:
Рассмотрим числитель дроби: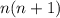 - произведение двух подряд идущих натуральных чисел, значит одно из них четное, а другое нечетное. Если четное число делится только на 2, но не делится на 4, то при вычислении значения дроби множитель "2" сократится и получившийся результат будет нечетным. Если четное число делится хотя бы на 4, то при вычислении значения дроби один множитель "2" сократится, но еще как минимум один множитель "2" останется и результат будет четным.
- произведение двух подряд идущих натуральных чисел, значит одно из них четное, а другое нечетное. Если четное число делится только на 2, но не делится на 4, то при вычислении значения дроби множитель "2" сократится и получившийся результат будет нечетным. Если четное число делится хотя бы на 4, то при вычислении значения дроби один множитель "2" сократится, но еще как минимум один множитель "2" останется и результат будет четным.
Итак, для четного результата сложения необходимо, чтобы хотя бы один из множителей произведения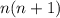 делился на 4.
делился на 4.
1 случай: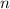 делится на 4 (или же можно сказать, что
делится на 4 (или же можно сказать, что 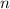 при делении на 4 дает остаток 0).
при делении на 4 дает остаток 0).
2 случай: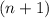 делится на 4, тогда
делится на 4, тогда 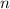 при делении на 4 дает остаток 3.
при делении на 4 дает остаток 3.
Если эти условия не выполняются, то результат сложения будет нечетным. То есть, можно сказать, что это происходит, когда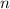 при делении на 4 дает остаток 1 или 2.
при делении на 4 дает остаток 1 или 2.
ответ: четный результат - когда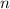 при делении на 4 дает в остатке 0 или 3; нечетный результат - когда
при делении на 4 дает в остатке 0 или 3; нечетный результат - когда 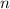 при делении на 4 дает в остатке 1 или 2.
при делении на 4 дает в остатке 1 или 2.
первые n натуральных чисел - это арифметическая прогрессия с разностью равной 1 и таким же первым членом, тогда по формуле сумма первых n ее членов равна: ((n+1)*n)/2, эту формулу можно преобразовать следующим образом: n * (n+1)/2, для нечетного n и (n+1) * n/2, для четного n. В первом случае результат зависит от (n+1)/2, каким оно будет по четности, таким и будет результат, аналогично во втором случае все зависит от n/2. Нетрудно заметить, что и n/2 и (n+1)/2 чередуют свои четности с шагом 4, то есть если при n = 1 результат нечетный, то и при n = 5 результат тоже нечетный. Зная, что при n = 1 и n = 2 результаты нечетные, а при n = 3 и n = 4 четные, делаем вывод, что четность результата зависит от остатка при делении n на 4, а точнее, если остаток 1 или 2, то результат нечетный, а если 0 или 3, то четный.