Составьте уравнение касательной к графику функции f в точке М. F (х) = 2 х 2 + х 3 , М (-3;9) f(х) = х 3 - 2 х , М (3;9).
2).Тело движется по закону х(t) = t 4 +0,5 t2 – 3t , х(t) = t 3 - 2 t 2 + 5 ,
х- в метрах, t- в секундах
Найдите скорость и ускорение тела через 2 секунды после начала движения.
3).Найдите тангенс угла наклона касательной к графику функции f(х) в точке х 0 :
f(х) = 3 х 2 - 1 2 х + 5 , х0 = - 1, f(х) = 2 х 2 + 8 х - 3 , х0 = - 3.
Моторная лодка за одно и тоже время может проплыть 48 км по течению и 36 км против течения реки. Какова собственная скорость лодки, если скорость течения 2 км\час.
Пусть собственная скорость лодки - х км/ч. Тогда:
По течению: (x + 2) км/ч
Против: (x - 2) км/ч
Из формулы времени:
Так как время одно и тоже можем составить следующее уравнение:
48(x - 2) = 36(x + 2)
48x - 36x = 96 + 72
12x = 168
x = 14
Значит, собственная скорость лодки 14 км/ч
ответ: 14 км/ч
Пусть
км/ч - это скорость моторной лодки.
__________________________________________
По течению: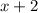
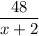
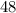
Против течения: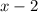
__________________________________________
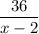
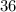
Так как, по условию, пути в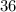
км и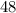 
км (против течения и по течению соответственно) были преодолены за одинаковое время, то имеем равенство двух промежутков времен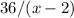и (
и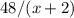 
) вместе с уравнением:
Значит, скорость моторной лодки -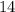
км/ч.
Задача решена!
ответ: 14 км/ч.