Предлагаю заменить
Тогда:
Получаем
p=- 5; p=4.
р>0 => p=4
Перейдем к начальной системе:
Решим второе уравнение системы:
- по Т.Виета
Отсюда, подставляя получаем:
Предлагаю заменить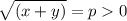
Тогда: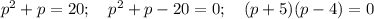
Получаем
p=- 5; p=4.
р>0 => p=4
Перейдем к начальной системе: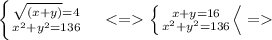
Решим второе уравнение системы:
Отсюда, подставляя получаем:
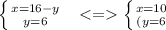
ОТВЕТ: (6;10); (10; 6)