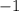Шал шалқанды жерден суырып алмақшы болғанда тарту күшін 600Н жеткізеді, кемпір 100Н дейін, немересі 50Н дейін, ит 30 Н дейін, мысық 10 Н дейін жеткізеді. Шалқанды шығара алмаған соң мысық тышқанды шақырады. Тышқанның тарту күші 2 Н. Олар шалқанды тарта-тарта ақыры шығарады. Қорытқы күш векторының модулі неге тең және бағыты қалай бағытталады? Егер шалқанды жерде ұстап тұрған күш 791 Н болса, осы топ тышқансыз шығара алар ма ед
в) 8у-5z=23 24y -15z = 69
3у-2z=6 -24y + 16z = -48
z = 21
y = (23+5z) / 8 = (23 + 5*21) / 8 = (23+105) / 8 = 128 /8 = 16.
Проверка: 3у-2z=6
3*16 - 2*21 = 48 - 42 = 6
г) 13x-15у= -48 26х - 30у = -96
2x+y =29 -26х - 13у = -377
-43у = -473 у = 11
х = (15у - 48) / 13 = (15*11 - 48) / 13 = (165 - 48) / 13 = 117 / 13 = 9.
Проверка: 2x+y =29
2*9 + 11 = 18 + 11 = 29.
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)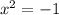
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)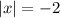
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)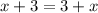
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: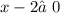 ,
, 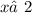 ;
;
ответ: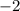
2)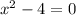
ответ: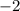 ;
; 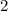
=> уравнения не равносильные.
10. 1)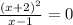
ОДЗ: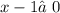 ,
, 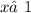 ;
;
ответ: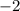
2)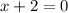
ответ: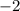
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12.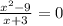
ОДЗ: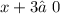 ,
,  ;
;
ответ: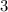
13.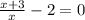
ОДЗ: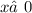 ;
;
ответ: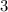
14.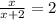
ОДЗ: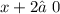 ,
,  ;
;
ответ: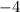
15.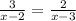
ОДЗ: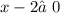 ,
, 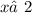 ,
, 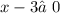 ,
, 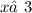 ;
;
ответ:
16.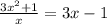
ОДЗ: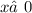 ;
;
ответ: