с заданием Решите неравенство sin>

1)

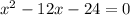
данное уравнение имеет два различных корня.

по теореме Виета:

Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.

2)

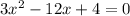
уравнение имеет два различных корня.

по теореме Виета:

Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.

3)

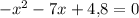
уравнение имеет два различных корня. По т. Виета:

Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.

4)

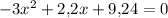
уравнение имеет два различных корня. По т. Виета:

Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.

Вариант Б1:

Дано:

АО=DO

<1=<2

Док-ть: тр. АОВ=тр. DOC

Доказательство:

1) <ВАО+<1 = 180° (смежные)

<CDO+<2 = 180° (смежные)

<ВАО = 180 - <1

<CDO = 180 - <2

Т.к. <1 и <2 равны (по усл.), то:

<BAO=<CDO

2) Рассмотрим тр-ки AOB и DOC:

<BAO=<CDO (доказано)

<BOA = <COD (вертик.)

AO=DO (по усл.)

Значит,

тр AOB = тр DOC

Доказано.

Дано:

ABCD — четырехугольник

AD=BC, AB = CD

Доказать: <А = <С

Доказательство:

1) Доп. построение — диагональ BD

2) Рассм. тр-ки ABD и CBD:

AD = BC, AB = CD (по усл.)

BD — общая.

Значит,

тр ABD = тр CBD

3) В равных треугольниках все соответствующие элементы равны.

Значит,

<A = <C

<A = <CДоказано.

Дано:

ABCD — четырёхугольник

BD, AC — диагонали.

тр ABC = тр CDA

Доказать: тр ABD = тр CDB

Доказательство:

1) Т. к. тр-ки ABC и CDA равны, то:

AD = BC

AB = CD

2) Рассмотрим тр-ки ABD и CDB:

AD = BC, AB = CD (док.)

BD — общая

Значит,

тр ABD = тр CDB

Доказано.