С. тема : "вычисление производной" : 1. найдите тангенс угла ф между касательной к графику функций y=2 tg x в точке с абсциссой x0=число пи/4 и положительным направлением оси ox 2.при каких значение х выполняет равенство
f'(x)=0 если известно, что f(x)=10 корень из x -x+3?
1) f '(x0) является угловым коэффициентом касательной к графику функции у = f(x) в точке x0. Угловой коэффициент прямой равен тангенсу угла, образованного этой прямой с положительным направлением оси Ох.
tg φ = -4 - тангенс угла ф между касательной к графику функции
2)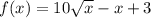
Найдем производную
ОДЗ: x≥0
x = 25
при x = 25