Рассмотрим остатки отделения чисел вида (10^n-1)/9 на 2021. Количество возможных остатков конечно, а это значит, что найдутся такие числа и , для которых остатки от деления равны. Поэтому если вычесть одно число из другого, то остаток от деления полученной разницы на 2021 будет равен 0. Полученное число будет иметь вид 11...11*10^n. Но 2021 не делится ни на 5, ни на 2. Из этого следует, что число 11..11 делится на 2021.
Теорема Эйлера позволяет найти длину числа 11..11, которое делится на 2021. Это 1932. Но это не минимальное n, (10^966-1)/9 тоже делится на 2021.
Да, найдется
Объяснение:
Рассмотрим остатки отделения чисел вида (10^n-1)/9 на 2021. Количество возможных остатков конечно, а это значит, что найдутся такие числа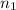
и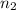 
, для которых остатки от деления равны. Поэтому если вычесть одно число из другого, то остаток от деления полученной разницы на 2021 будет равен 0. Полученное число будет иметь вид 11...11*10^n. Но 2021 не делится ни на 5, ни на 2. Из этого следует, что число 11..11 делится на 2021.
Теорема Эйлера позволяет найти длину числа 11..11, которое делится на 2021. Это 1932. Но это не минимальное n, (10^966-1)/9 тоже делится на 2021.
Надеюсь
Объяснение:
Номер 103:
Пусть первый цех изготовил х деталей, тогда второй 3х, а третий 1,5х
х + 3х + 1,5х = 729
5,5х = 729
х = 144 - деталей изготовил первый цех
144 × 3 = 432 - деталей изготовил второй цех
432 ÷ 2 = 216 - деталей изготовил третих цех
Номер 104:
Пусть каждая боковая сторона равнобедренного треугольника равна x см.
Основание составляет 3/4 боковой стороны или 0,75x см.
Известно, что периметр равен 22 см.
Решаем уравнение.
2x + 0,75x = 22,
2,75x = 22,
x = 22 : 2,75,
x = 8 (см) - боковая сторона.
0,75 * 8 = 6 (см) - основание.
ответ: Стороны треугольника 8 см, 8 см и 6 см.
Номер 105:
120 ÷ 2 = 60м полуметр (длины двух смежных сторон)
х ширина
2х длина
х + 2х = 60
х = 20м ширина
20 × 2 = 40м длина