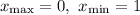[у²/(у²-6уb)] : [y/(y²-36b²)]= 17 при у=5-6√3; b=2+√3.
В первом знаменателе вынести у за скобки, во втором знаменателе разность квадратов, развернуть:
=[у²/у(у-6b)] : [y/(y-6b)(у+6b)]=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой меняет знак с "+" на "–" (двигаясь в направлении увеличения ), то — точка максимума, а если с "–" на "+" , то — точка минимума.
17.
Объяснение:
Найти значение выражения:
[у²/(у²-6уb)] : [y/(y²-36b²)]= 17 при у=5-6√3; b=2+√3.
В первом знаменателе вынести у за скобки, во втором знаменателе разность квадратов, развернуть:
=[у²/у(у-6b)] : [y/(y-6b)(у+6b)]=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
=[y²*(y-6b)(у+6b)] / [у(у-6b)*y]=
Сокращение у, у и у²; (y-6b) и (y-6b) на (y-6b):
=у+6b=
=5-6√3+6(2+√3)=
=5-6√3+12+6√3=
=5+12=17.
Необходимые условия экстремума:
Имеем две критические (стационарные) точки: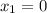
и 
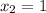
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой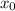
меняет знак с "+" на "–" (двигаясь в направлении увеличения 
), то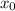 
— точка максимума, а если с "–" на "+" , то 
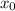— точка минимума.
Из промежутка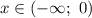
выберем, например, 
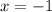и имеем: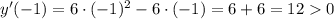 
Из промежутка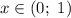
выберем, например, 
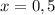и имеем: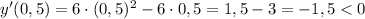 
Имеем максимум в точке с абсциссой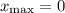
Из промежутка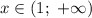
выберем, например, 
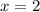и имеем: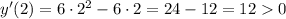 
Имеем минимум в точке с абсциссой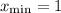
ответ: