Алгебра: Решите систему: cos(x)*sin(y)=1/4 sin(x)*cos(y)=3/4

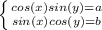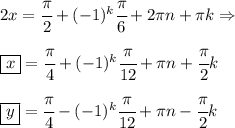
Решение:Во-первых, необходимо, следуя формуле , сложим и вычтим уравнения системы и получим равносильную систему.Теперь по формуле синусов рассмотрим систему в более банальной форме.Теперь сложим первое и второе уравнения и получим далее по алгоритму результат.ответ: ...

Решите систему: cos(x)sin(y)=1/4
sin(x)cos(y)=3/4

Показать ответ

Ответ:

krikovaluba

12.10.2020 23:01

Решение:

Во-первых, необходимо, следуя формуле $\left \{ {{cos(x)sin(y)=a} \atop {sin(x)cos(y) = b}}$ , сложим и вычтим уравнения системы и получим равносильную систему.

$\left \{ {{sin(x-y)=\cfrac{3-1}{4}}} \atop {sin(x+y) = \cfrac{1+3}{4}} \right.\Rightarrow \left \{ {{sin(x-y)=\cfrac{2}{4}\rightarrow \cfrac{1}{2}}} \atop {sin(x+y) = \cfrac{4}{4}\rightarrow1}\left \right.$

Теперь по формуле синусов рассмотрим систему в более банальной форме.

$\left \{ {{sin(x-y)=\cfrac{1}{2}} \atop {sin(x+y)=1}} \right. \Rightarrow \left \{ {{x-y=(-1)^k \cfrac{\pi}{6}+\pi k} \atop {x+y=\cfrac{\pi}{2}+2\pi n}}\right.$

Теперь сложим первое и второе уравнения и получим далее по алгоритму результат.

$2x=\cfrac{\pi}{2}+(-1)^k \cfrac{\pi}{6} +2\pi n + \pi k \Rightarrow \\ \\ \boxed{x}=\cfrac{\pi}{4}+(-1)^k \cfrac{\pi}{12}+\pi n + \cfrac{\pi}{2} k \\ \\ \boxed{y}=\cfrac{\pi}{4}-(-1)^k \cfrac{\pi}{12}+\pi n - \cfrac{\pi}{2} k$

ответ: $\boxed{\bf x=\cfrac{\pi}{4}+(-1)^k \cfrac{\pi}{12}+\pi n + \cfrac{\pi}{2} k; \: \: y=\cfrac{\pi}{4}-(-1)^k \cfrac{\pi}{12}+\pi n - \cfrac{\pi}{2} k}$