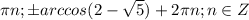Войти Регистрация Спроси ai-bota

Решите очень
2sin2x+sin^3x=0

Показать ответ

Ответ:

жыландыыыы

15.10.2020 13:41

$2sin2x+sin^3x=0\\2*2sinxcosx+sin^3x=0\\sinx(4cosx+sin^2x)=0\\sinx(4cosx+1-cos^2x)=0$

$sinx=0: x=\pi n, n\in{Z}$

или

$4cosx+1-cos^2x=0\\cos^2x-4cosx-1=0\\D=16+4=20\\cosx=\frac{4\pm\sqrt{20} }{2}\\ cosx=\frac{4\pm2\sqrt{5} }{2}\\cosx=2\pm\sqrt{5}$

$cosx=2+\sqrt{5}$ - решений не имеет, так как $|cosx|\leq 1$ , а $2+\sqrt{5}1$

$cosx=2-\sqrt{5}: x=\pm{arccos(2-\sqrt{5} )}+2\pi n, n\in{Z}$

ответ: $\pi n;\pm{arccos(2-\sqrt{5} )}+2\pi n; n\in{Z}$

0,0(0 оценок)

Популярные вопросы: Алгебра

kseniaGksenia

09.04.2022 08:05

А)(√4)²-1,5 б)7×(√2/7)² в)(√0,9)²-0,3 г)1/6×(√12)²д)√4²+33е)√4×5²-6²ж)√3(0,4²+0,11)з)√0,5²-0,3²...

catikis

30.10.2021 10:21

Доведи разложение на множители до конца: x^2+8x+15 = x^2 + 5x + 3x + 15 = .....

ДанилКаДми

17.04.2020 08:49

Шкив радиусом 60 мм делает 300 об/мин. С каким ускорением движется точка на его ободе? Какой линейной скоростью обладает эта точка? Чему равна её угловая скорость Это физика...

оаиьлжщ

06.12.2020 19:00

Перетворіть вираз в одночлен стандартного вигляду:...

Апслтел

12.02.2022 04:05

Розв яжіть рівняння: 3х (3-х) +3х2 = -189...

sopyryaeva1976

14.08.2021 23:00

тому кто помежет решить найти наименьший положительный период функции y=cos 5/3x...

daniel9876

15.12.2022 10:35

Какая функция является первообразной для функции f(x)=sin2x...

kristinamoroz1

20.08.2020 00:16

Решите уравнения: 3х-6/11=0 4(2-4х)+6х=3 9х=5х-(72-2х) (х-4)*(1+х)=0 решите : в двух папках было одинаковое кол-во тетрадей. после того, как из второй папки переложили в...

лолkjk

20.08.2020 00:16

Мама хочет наказать петю за двойку по .они договорились о следующем.петя задумывает двузначное число с разными цифрами и сообщает его маме.после этого мама называет свое...

anastasiyanast29

20.08.2020 00:16

1)раскройте скобки и подобные слагаемые в выражении (1,3a-+2,7a) 2)преобразуйте выражение 2,5(-2x+4y-z) в тождественно равное...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку