Объяснение:
Пусть
Найдём нули левой части:
Решение неравенства:
Заметим, что при любых z. Тогда достаточно решить неравенство
Заметим, что меньший корень отрицателен, а z по замене всегда положительно. Значит, решение неравенства достаточно записать как
Объяснение:
Пусть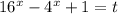
Найдём нули левой части:
Решение неравенства:
Пусть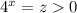
Заметим, что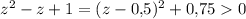 при любых z. Тогда достаточно решить неравенство
при любых z. Тогда достаточно решить неравенство
Найдём нули левой части:
Заметим, что меньший корень отрицателен, а z по замене всегда положительно. Значит, решение неравенства достаточно записать как