Эта функция дифференцируема на всех числовой прямой, она будет убывающей, если её производная ≤ 0 на всей числовой прямой (при этом ни на каком отрезке производная не должна быть тождественно равна нулю, иначе она на этом промежутке не будет меняться)
y' = -3x^2 + 2px - 3 ≤ 0
У квадратного трёхчлена старший коэффициент меньше нуля, поэтому чтобы неравенство было выполнено при всех x, дискриминант должен быть неположительным.
y' = -3x^2 + 2px - 3 ≤ 0
У квадратного трёхчлена старший коэффициент меньше нуля, поэтому чтобы неравенство было выполнено при всех x, дискриминант должен быть неположительным.
D/4 = (2p/2)^2 - (-3) * (-3) = p^2 - 9 ≤ 0
p^2 ≤ 9
-3 ≤ p ≤ 3
ответ. при -3 ≤ p ≤ 3.
№1.
Объяснение:
Пусть сторона 1-го квадрата равна А, а сторона 2-го равна В. Тогда можно составить систему уравнений:
Выражаем значение одной из переменных из 1-го уравнения и подставляем во 2-е:
Домножим все слагаемые на B^2, и затем заменим B^2 на t:
Значение t1 меньше 0, что не соответствует здравому смыслу, поэтому его не рассматриваем.
ответ: 3 и 4 см
-----------------
№2.
Объяснение:
Пусть один катет равен a, второй равен b. Тогда, исходя из теоремы Пифагора, составим систему уравнений:
Выразим одну из переменных из 2-го уравнения и подставим в 1-е:
Таким образом, катеты равны 5 и 12 см. Площадь такого треугольника будет равна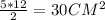
ответ: 30 см^2