Пусть сторона квадрата равна . Тогда по условию, Теперь попробуем найти стороны треугольника PQD:
1) найти PD:
По теореме Пифагора
2) найти PQ и QD:
Проведем прямую проходящую через точку Q и параллельную BC, и отметим точки пересечения с квадратом ABCD как M и N где M∈AB, N∈CD и прямую проходящую через точку Q и параллельную AB, пересекающую квадрат в точках E и F где E∈BC, F∈AD.
Тогда из параллельности PQ||BC, FQ||CD и свойства пропорциональных отрезков получаем,
Следовательно из ,
Также из-за того, что AP<AM,
Заметим что, AMQF - прямоугольник, тогда
Теперь нам известны катеты прямоугольных треугольников PMQ и QFD, значит мы можем найти и их гипотенузы PQ и QD,
3) доказать что ∠PQD=90°:
Действительно,
Из обратной теоремы Пифагора следует что, ∠PQD - прямой угол.
4) доказать что ∠PQD - наибольший угол соответствующего треугольника:
Предположим обратное, допустим в треугольнике PQD есть угол больший 90°, но тогда сумма углов этого треугольника будет больше 180° - противоречие.
По итогу имеем то что, ∠PQD=90° - наибольший угол треугольника PQD.
Обозначим C - массу меди в сплаве и S - массу олова в сплаве.
Тогда условие задачи
"Имеется сплав меди и олова массой 40 кг. "
запишем алгебраически:
C + S = 40
При этом, если обозначить за X - то, что нам нужно найти, то есть процентное содержание олова в первоначальном сплаве, можем записать, что C = 40 * X, для S будет, соответственно, S = 40 (1-X).
То есть X = C/40.
Продолжим читать условие и записывать его алгебраически:
"При добавлении 5кг меди процентное содержание меди увеличилось на 10 процентных пунктов".
C + 5 = (40 + 5) * (X + 0.1)
Найдем С, подставив Х = C/40:
C + 5 = 45 (C/40 + 0.1)
C + 5 = 45C/40 + 4.5
9C/8 - C = 5 - 4.5
C/8 = 0.5
C = 4
Итак, мы нашли массу меди в исходном сплаве, тогда можем найти ответ подставив вычисленное значение в формулу для процентного содержания олова в первоначальном сплаве:
90 градусов.
Объяснение:
Пусть сторона квадрата равна
. Тогда по условию,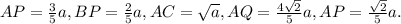 
Теперь попробуем найти стороны треугольника PQD:
1) найти PD:
По теореме Пифагора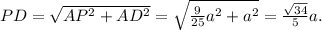
2) найти PQ и QD:
Проведем прямую проходящую через точку Q и параллельную BC, и отметим точки пересечения с квадратом ABCD как M и N где M∈AB, N∈CD и прямую проходящую через точку Q и параллельную AB, пересекающую квадрат в точках E и F где E∈BC, F∈AD.
Тогда из параллельности PQ||BC, FQ||CD и свойства пропорциональных отрезков получаем,
Следовательно из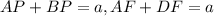
,
Также из-за того, что AP<AM,
Заметим что, AMQF - прямоугольник, тогда
Теперь нам известны катеты прямоугольных треугольников PMQ и QFD, значит мы можем найти и их гипотенузы PQ и QD,
3) доказать что ∠PQD=90°:
Действительно,
Из обратной теоремы Пифагора следует что, ∠PQD - прямой угол.
4) доказать что ∠PQD - наибольший угол соответствующего треугольника:
Предположим обратное, допустим в треугольнике PQD есть угол больший 90°, но тогда сумма углов этого треугольника будет больше 180° - противоречие.
По итогу имеем то что, ∠PQD=90° - наибольший угол треугольника PQD.
10%
Объяснение:
Обозначим C - массу меди в сплаве и S - массу олова в сплаве.
Тогда условие задачи
"Имеется сплав меди и олова массой 40 кг. "
запишем алгебраически:
C + S = 40
При этом, если обозначить за X - то, что нам нужно найти, то есть процентное содержание олова в первоначальном сплаве, можем записать, что C = 40 * X, для S будет, соответственно, S = 40 (1-X).
То есть X = C/40.
Продолжим читать условие и записывать его алгебраически:
"При добавлении 5кг меди процентное содержание меди увеличилось на 10 процентных пунктов".
C + 5 = (40 + 5) * (X + 0.1)
Найдем С, подставив Х = C/40:
C + 5 = 45 (C/40 + 0.1)
C + 5 = 45C/40 + 4.5
9C/8 - C = 5 - 4.5
C/8 = 0.5
C = 4
Итак, мы нашли массу меди в исходном сплаве, тогда можем найти ответ подставив вычисленное значение в формулу для процентного содержания олова в первоначальном сплаве:
X = C/40 = 4/40 = 0.1 или 10%.
ответ: 10%.