Алгебра: Решите, , кр по 8 класс сокращение дробей

Решите, , кр по 8 класс сокращение дробей

Показать ответ

Ответ:

dgfhdhdj95

05.04.2021 23:19

Пусть маленький коала ест со скоростью х листьев/час, тогда на дереве эвкалипта 10х листьев.
Известно, что каждый из родителей съедает листья в 2 раза быстрее, значит их скорость 2*х листьев / час.
Общая скорость поедания листьев (мамы, папы и сына) составляет
(х+2х+2х)=5х листьев/час. Время за которое они съедят все листья
10х:5х=2 часа ⇒ за 2 часа они съедят все листья Скорость маленькой панды 1/10 листьев/час.
1/10*2=1/5 листьев /час скорость мамы или папы
1/5*2+1/10=5/10=1/2 листьев/час - съедает все семейство
1:1/2=2 часа уйдет у семьи коал, чтобы съесть все листья с дерева

ответ 2 часа

0,0(0 оценок)

Ответ:

ba150704

14.08.2022 23:55

ответ: при р<0.

Решение: Данное в условии неравенство не будет иметь решений, если график функции (p-1)x^2+(p-2)x+(3p-1) будет целиком находитьcя ниже оси х.

В случае, если p=1, функция приобретает вид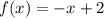 f(x)=-x+2 . Это линейная функция, графиком которой является прямая, пересекающая ось х (т.к. ее угловой коэффициент отличен от нуля). Но тогда неравенство будет иметь решения, так что $p\ne 1$ .

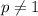В случаях, когда p не равно 1, графиком функции будет являться парабола. Нас интересует такая парабола, ветви которой направлены вниз и вершина которой находится ниже оси х (это будет означать отсутствие решений для неравенства из условия). Для этого требуется два условия:

1) p-1<0, т.е p<1:

2) дискриминант квадратного уравнения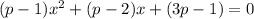 (p-1)x^2+(p-2)x+(3p-1)=0 меньше нуля.

Найдем дискриминант:

D=(p-2)^2-4(3p-1)(p-1)=p^2-4p+4-4(3p^2-p-3p+1)= =p^2-4p+4-12p^2+16p-4=-11p^2+12p=p(12-11p)

Итак, нам остается лишь решить неравенство p(12-11p)<0. Получаем p<0, либо p>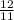 $\frac{12}{11}$ . Но второе решение неравенства не удовлетворяет условию p<1, поэтому оставляем p<0.