1) Т.к. это квадратичная функция, представленная параболой, найдем вершину параболы по следующей формуле:
Подставляем единичку в функцию:
2*1-4*1+1=2-4+1=2-3=-1.
Ниже график функции не будет подыматься, следовательно, множество значений:
y∈{-1...+∞}.
2)
Несмотря ни на что, под корнем НИКОГДА не должно быть отрицательное значение. Решаем 2 полноценных систем уравнения:
Но, -3<5 ⇒x≥5.
D(f)=x≥5
3) Вы, наверно, имели ввиду сумму корней.
Проведем замену переменной:
Решаем квадратное уравнение:
А теперь, решаем два уравнения:
Но, нежелательно в уравнение вставлять комплексные числа, т.е. второй вариант просто убираем. Получим единственный корень - √3.
Вся работа=1
За 1 день Количество дней на всю работу
1рабочий 1/(х+3) х+3
2 рабочий 1/х х
Первый за 1,5 дня делает 1,5*1/(х+3) работы.
Остальную работу делают вмести за 7-1,5=5,5 дней. 5,5*(1/х + 1/(х+3))
Составляем уравнение
-1.5 не удовлетворяет условию задачи
11 дней на всю работу 2 рабочему
11+3=14 дней 1 рабочему
ответ: 14 и 11 дней
1) Т.к. это квадратичная функция, представленная параболой, найдем вершину параболы по следующей формуле:
Подставляем единичку в функцию:
2*1-4*1+1=2-4+1=2-3=-1.
Ниже график функции не будет подыматься, следовательно, множество значений:
y∈{-1...+∞}.
2)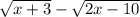
Несмотря ни на что, под корнем НИКОГДА не должно быть отрицательное значение. Решаем 2 полноценных систем уравнения:
Но, -3<5 ⇒x≥5.
D(f)=x≥5
3) Вы, наверно, имели ввиду сумму корней.
Проведем замену переменной:
Решаем квадратное уравнение:
А теперь, решаем два уравнения:
Но, нежелательно в уравнение вставлять комплексные числа, т.е. второй вариант просто убираем. Получим единственный корень - √3.
Вся работа=1
За 1 день Количество дней на всю работу
1рабочий 1/(х+3) х+3
2 рабочий 1/х х
Первый за 1,5 дня делает 1,5*1/(х+3) работы.
Остальную работу делают вмести за 7-1,5=5,5 дней. 5,5*(1/х + 1/(х+3))
Составляем уравнение
-1.5 не удовлетворяет условию задачи
11 дней на всю работу 2 рабочему
11+3=14 дней 1 рабочему
ответ: 14 и 11 дней