Ну давай начнем с того, что вообще такое область определения.
Область определения - область значений x (или любой другой независимой переменной), при котором функция имеет смысл, то есть имеет значение y
Функция не имеет значения (и значений тоже), когда, например, присутствует деление на 0, а так же, когда подкоренное выражение отрицательно (но последнее - только в рамках действительных чисел, но сейчас мы рассматриваем задачу в этих рамках, иначе это было-бы указано). Это мы сейчас и будем использовать.
11. Давай сразу посмотрим на знаменатели, остальное сейчас не имеет значения
не должен быть равен 0. Мы можем повлиять только на х, что и будем делать.
Сначала предположим, в каком случае знаменатель будет равен 0
Квадратный корень равен нулю, когда подкоренное выражение равно нулю, тогда
когда , => (следовательно) , а такого не бывает. Этот параметр не задает никаких условий к области определения.
Тогда, посмотрим на другое условие - подкоренное выражение не должно быть отрицательным, значит должен быть больше или равен нулю, значит, , следовательно, => => => и (это - исключительно совокупность)
Значит, из этого знаменателя мы можем вынести, что и (если-бы было еще что-то, то данное условие вошло бы с ним в еще одну совокупность)
Посмотрим тогда на знаменатель другой дроби
Здесь все проще - x-1
Тут нет квадратного корня, поэтому - единственное, на что можно обратить внимание - это то, что знаменатель дроби не должен быть равен нулю.
Предположим, что знаменатель равен нулю, тогда x-1=0 => x=1
Так как при этом значении х функция утрачивает смысл, то это значение надо исключить из области определения =>
Итак, мы имеем два условия, при соблюдении которых функция будет иметь смысл- и и (последнее- совокупность). При этом, если соблюсти только одно из условий - функция все равно не будет иметь значений. Значит, это тоже будет совокупностью.
Если надо, можно записать в таком виде - (нижнюю строку надо тоже сделать совокупностью, я не могу это сделать на компьютере)
Или так - x ∈ [-2;0)∩(0;2]
В целом, действовать можно по такой схеме - находим знаменатели дробей, смотрим, есть ли в них переменная, если есть - то находим область значений этой переменной, при которых значение знаменателя не будет равно нулю (на промежуточном этапе можно в виде n). Потом - ищем корни, и находим область определения, при котором подкорное выражение неотрицательное. Потом - объединяем полученные условия в совокупность - и готово
См в объяснение, это полезно
Объяснение:
Ну давай начнем с того, что вообще такое область определения.
Область определения - область значений x (или любой другой независимой переменной), при котором функция имеет смысл, то есть имеет значение y
Функция не имеет значения (и значений тоже), когда, например, присутствует деление на 0, а так же, когда подкоренное выражение отрицательно (но последнее - только в рамках действительных чисел, но сейчас мы рассматриваем задачу в этих рамках, иначе это было-бы указано). Это мы сейчас и будем использовать.
11. Давай сразу посмотрим на знаменатели, остальное сейчас не имеет значения
Сначала предположим, в каком случае знаменатель будет равен 0
Квадратный корень равен нулю, когда подкоренное выражение равно нулю, тогда
Тогда, посмотрим на другое условие - подкоренное выражение не должно быть отрицательным, значит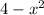 должен быть больше или равен нулю, значит,
должен быть больше или равен нулю, значит, 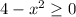 , следовательно,
, следовательно, 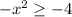 =>
=>  =>
=> 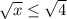 =>
=> 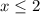 и
и 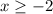 (это - исключительно совокупность)
(это - исключительно совокупность)
Значит, из этого знаменателя мы можем вынести, что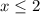 и
и 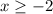 (если-бы было еще что-то, то данное условие вошло бы с ним в еще одну совокупность)
(если-бы было еще что-то, то данное условие вошло бы с ним в еще одну совокупность)
Посмотрим тогда на знаменатель другой дроби
Здесь все проще - x-1
Тут нет квадратного корня, поэтому - единственное, на что можно обратить внимание - это то, что знаменатель дроби не должен быть равен нулю.
Предположим, что знаменатель равен нулю, тогда x-1=0 => x=1
Так как при этом значении х функция утрачивает смысл, то это значение надо исключить из области определения =>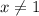
Итак, мы имеем два условия, при соблюдении которых функция будет иметь смысл-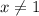 и
и 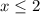 и
и 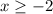 (последнее- совокупность). При этом, если соблюсти только одно из условий - функция все равно не будет иметь значений. Значит, это тоже будет совокупностью.
(последнее- совокупность). При этом, если соблюсти только одно из условий - функция все равно не будет иметь значений. Значит, это тоже будет совокупностью.
Если надо, можно записать в таком виде -![x=\left[\begin{array}{ccc}x\neq 1\\x\leq 2&x\geq -2\end]](/tpl/images/1495/6656/00f1e.png) (нижнюю строку надо тоже сделать совокупностью, я не могу это сделать на компьютере)
(нижнюю строку надо тоже сделать совокупностью, я не могу это сделать на компьютере)
Или так - x ∈ [-2;0)∩(0;2]
В целом, действовать можно по такой схеме - находим знаменатели дробей, смотрим, есть ли в них переменная, если есть - то находим область значений этой переменной, при которых значение знаменателя не будет равно нулю (на промежуточном этапе можно в виде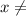 n). Потом - ищем корни, и находим область определения, при котором подкорное выражение неотрицательное. Потом - объединяем полученные условия в совокупность - и готово
n). Потом - ищем корни, и находим область определения, при котором подкорное выражение неотрицательное. Потом - объединяем полученные условия в совокупность - и готово
Затем формулы двойного угла
sin2α=2sinαcosα
cos2α=cos²α-sin²α=cos²α-(1-cos²α)=2cos²α-1⇒ 2cos²α=1+cos2α
cos2α=cos²α-sin²α=1-sin²α-sin²α=1-2sin²α⇒ 2sin²α=1-cos2α
а) сos75°cos105°=cos(90°-15°)·cos(90°+15°)=
= sin15°(-sin15°)=-sin²15°=-(1-cos30°)/2=(cos30°-1)/2=
((√3/2)-1)/2=0,25√3-0,5
б) sin75°sin15°=°sin(90°-15°)sin15°=cos15°sin15°=sin30°/2=1/4=0,25
в) sin105°cos15°=sin(180°-75°)cos15°=sin75°cos15°=sin(90°-15°)cos15°=cos15°cos15°=(1+cos30°)/2=(1+(√3/2))/2=0,5 +0,25√3
Формулы
cosα·cosβ=0,5cos(α-β)+0,5cos(α+β)
sinα·sinβ=0,5cos(α-β)-0,5cos(α+β)
sinα·cosβ=0,5sin(α+β)+0,5sin(α-β)
а) сos75°cos105°=0,5cos(75°-105°)+0,5cos(75°+105°)=0,5cos(-30°)+0,5 cos180°=
=0,5·√3/2+0,5·(-1)=0,25√3-0,5
б) sin75°sin15°=0,5cos(75°-15°)-0,5cos(75°+15°)=0,5cos60°-0,5 cos90°=0,5·0,5=0,25
в) sin105°cos15°=0,5sin(105°+15°)+0,5sin(105°-15°)= =0,5sin120°+0,5sin90°=
=0,5 sin(180°-60°)+0,5·1=0,5 sin 60°+0,5=0,25√3+0,5