Пусть (км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в километров, равно часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это часов, минут или же часа = часа. И последний промежуток, часов ( километров со скоростью км/ч).
Теперь, конечно, будем решать уравнение:
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Общий вид квадратного трехчлена: y = ax² + bx + c и координаты любой точки (в том числе и вершины) должны обращать это выражение в верное равенство... т.е. нужно просто подставить координаты точек и решить систему из трех уравнений... чтобы найти конкретные значения коэффициентов (a, b, c))) y2 = a(x2)² + b*(x2) + c, для точки с координатами (х2, у2) y1 = a(x1)² + b*(x1) + c y0 = a(x0)² + b*(x0) + c, где (х0, у0) -- вершина причем х0 = -b / (2a) и это можно использовать как одно из трех уравнений системы)))
Пусть
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в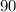
километров, равно 
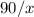часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это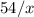
часов, 
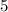минут или же 
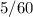часа = 
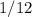часа. И последний промежуток, 
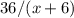часов (
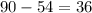километров со скоростью 
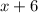км/ч).
Теперь, конечно, будем решать уравнение:
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -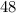
км/ч.
Задача решена!
ответ: 48 км / ч .y = ax² + bx + c
и координаты любой точки (в том числе и вершины) должны обращать это выражение в верное равенство...
т.е. нужно просто подставить координаты точек и решить систему из трех уравнений...
чтобы найти конкретные значения коэффициентов (a, b, c)))
y2 = a(x2)² + b*(x2) + c, для точки с координатами (х2, у2)
y1 = a(x1)² + b*(x1) + c
y0 = a(x0)² + b*(x0) + c, где (х0, у0) -- вершина
причем х0 = -b / (2a)
и это можно использовать как одно из трех уравнений системы)))