1)
нет решений
2)
3)
, где - целое число
Пошаговое объяснение:
Здравствуйте!
Очевидно, что
Заметим, что число - простое ( сначала будет считать, что , в силу того, что квадрат неотрицателен), а также, что x не делится на
Тогда, согласно малой теореме Ферма имеем:
( дает при делении на остаток )
Возведем обе части равенства в степень:
Поскольку в биноме Ньютона : каждый член, помимо члена , помножен на некоторую натуральную степень числа , то , поскольку - нечетное.
Таким образом, дает при делении на остаток или , то есть мы пришли к противоречию, а значит решений в целых числах нет.
Очевидно, что ,поскольку в противном случае левая часть равенства нецелое число, а правая часть равенства целое число.
Предположим, что , тогда делится на , а значит дает при делении на 4 дает остаток 1.
Левая часть равенства число нечетное, но тогда и - нечетное, а значит - также нечетное.
, где целое число
, где -целое число
Таким образом, дает при делении на остаток , но дает при делении на 4 остаток 1, то есть мы пришли к противоречию.
Откуда:
Проверим
Решений в целых числах нет.
То есть решение уравнения :
Разложим квадратный трехчлен из правой части на множители:
Поскольку, число простое , то хотя бы один из членов или делится на 3
Необходимо заметить, что если делится , то , также делится на 3 , а значит 5y+5-6 =5y-1 делится на 3.
Обратное утверждение также верно, если делится на , то делится на 3.
делится на , а поскольку
и -взаимнопростые, то делится на 3
Таким образом , для существования целых решений необходимо и достаточно, чтобы делилось на
, где - целое число.
Таким образом, данное уравнение имеет бесконечно много целых решений:
, где - целое число (может быть равно 0)
Возможно, в последнем уравнении есть ошибка, ибо очень просто.
Если вам понравился ответ, сделай его лучшим!
1)
нет решений
2)
3)
Пошаговое объяснение:
Здравствуйте!
1)
Очевидно, что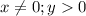
Заметим, что число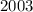 - простое ( сначала будет считать, что
- простое ( сначала будет считать, что 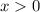 , в силу того, что квадрат неотрицателен), а также, что x не делится на
, в силу того, что квадрат неотрицателен), а также, что x не делится на
Тогда, согласно малой теореме Ферма имеем:
Возведем обе части равенства в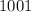 степень:
степень:
Поскольку в биноме Ньютона :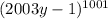 каждый член, помимо члена
каждый член, помимо члена 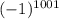 , помножен на некоторую натуральную степень числа
, помножен на некоторую натуральную степень числа 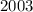 , то
, то 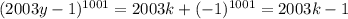 , поскольку
, поскольку 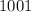 - нечетное.
- нечетное.
Таким образом,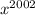 дает при делении на
дает при делении на 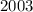 остаток
остаток 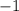 или
или 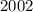 , то есть мы пришли к противоречию, а значит решений в целых числах нет.
, то есть мы пришли к противоречию, а значит решений в целых числах нет.
2)
Очевидно, что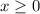 ,поскольку в противном случае левая часть равенства нецелое число, а правая часть равенства целое число.
,поскольку в противном случае левая часть равенства нецелое число, а правая часть равенства целое число.
Предположим, что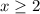 , тогда
, тогда 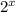 делится на
делится на 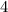 , а значит
, а значит 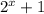 дает при делении на 4 дает остаток 1.
дает при делении на 4 дает остаток 1.
Левая часть равенства число нечетное, но тогда и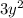 - нечетное, а значит
- нечетное, а значит 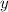 - также нечетное.
- также нечетное.
Таким образом,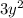 дает при делении на
дает при делении на 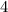 остаток
остаток 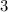 , но
, но 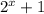 дает при делении на 4 остаток 1, то есть мы пришли к противоречию.
дает при делении на 4 остаток 1, то есть мы пришли к противоречию.
Откуда: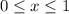
Проверим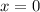
Решений в целых числах нет.
Проверим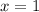
То есть решение уравнения :
3)
Разложим квадратный трехчлен из правой части на множители:
Поскольку, число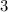 простое , то хотя бы один из членов
простое , то хотя бы один из членов 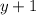 или
или 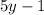 делится на 3
делится на 3
Необходимо заметить, что если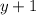 делится
делится 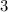 , то
, то 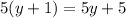 , также делится на 3 , а значит 5y+5-6 =5y-1 делится на 3.
, также делится на 3 , а значит 5y+5-6 =5y-1 делится на 3.
Обратное утверждение также верно, если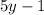 делится на
делится на 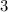 , то
, то 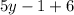 делится на 3.
делится на 3.
Таким образом , для существования целых решений необходимо и достаточно, чтобы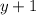 делилось на
делилось на 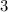
Таким образом, данное уравнение имеет бесконечно много целых решений:
Возможно, в последнем уравнении есть ошибка, ибо очень просто.
Если вам понравился ответ, сделай его лучшим!