1-ое уравнение:
2-ое уравнение:
Объяснение:
разложение на множители):
Заметим, что данное уравнение хорошо раскладывается на множители:
Второй множитель не имеет корней.
Поэтом ответ .
Поделим исходное уравнение на 28. Получим:
, где
Выполним вычисления:
Тогда действительный корень будет равен:
Пришли к тому же ответу.
Уравнение решено!
2)
(x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)
Раскроем скобки и упростим вырождение:
Второе уравнение раскладывается на множители:
Последнее кубическое уравнение не имеет целых корней.
Поэтому нужно считать так же, как мы делали это при решении 1-ого уравнения 2-ым
Значит имеем 3 корня:
Итого, уравнение имеет 5 корней:
Задание выполнено!
1-ое уравнение:
2-ое уравнение:
Объяснение:
разложение на множители):
Заметим, что данное уравнение хорошо раскладывается на множители:
Второй множитель не имеет корней.
Поэтом ответ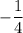 .
.
Поделим исходное уравнение на 28. Получим:
Выполним вычисления:
Тогда действительный корень будет равен:
Пришли к тому же ответу.
Уравнение решено!
2)
(x²+4x)(x²+x-6)=(x³-16x)(x²-2x-35)
Раскроем скобки и упростим вырождение:
Второе уравнение раскладывается на множители:
Последнее кубическое уравнение не имеет целых корней.
Поэтому нужно считать так же, как мы делали это при решении 1-ого уравнения 2-ым
Значит имеем 3 корня:
Итого, уравнение имеет 5 корней:
Задание выполнено!