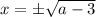Решить уравнение в зависимости от параметра a sqrt(x^2 - вопрос №213596611 от ivkn1401 08.04.2022 04:25

Question

Алгебра: Решить уравнение в зависимости от параметра a sqrt(x^2 + a) - sqrt(3a - 6 - x^2) = 0

ivkn1401 · Answer

Объяснение:Условие:Основное уравнение:Если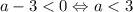 , уравнение решений не имеетЕсли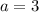 , уравнение имеет единственное решение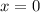 Если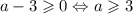 , уравнение имеет два решения...