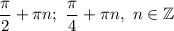1. Раскроем модуль при условии :
Однако корни не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:
2. Раскроем модуль при условии :
Заметим, что первое уравнение не удовлетворят условию раскрытия модуля. Продолжаем решать только второе уравнение:
Однако корни не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:
3. Объединим решения, полученные в предыдущих пунктах:
Или более кратко:
ответ:
1. Раскроем модуль при условии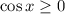 :
:
Однако корни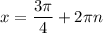 не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:
не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:
2. Раскроем модуль при условии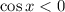 :
:
Заметим, что первое уравнение не удовлетворят условию раскрытия модуля. Продолжаем решать только второе уравнение:
Однако корни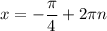 не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:
не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:
3. Объединим решения, полученные в предыдущих пунктах:
Или более кратко:
ответ: