решить систему:
2a1+5d=-17
(a1+d)(a1+3d)=40

13^26+9^20
Чтобы доказать что данное выражение делится на 10 достаточно доказать что сумма последних чисел будет оканчиваться на 0
Зная что, число 3 при возведение в степень оканчивается на
3^1=3
3^2=9
3^3=27 оканчивается на 7
3^4=81 оканчивается на 1
3^5=243 оканчивается на 3 и так будет повторятся через каждый 4 порядка ... следовательно в 26 степени число будет оканчиваться на 9
9^20=3^40 и исходя из вышеизложенного 3 в 40 степени будет оканчиваться на 1 получается
9+1=0 следовательно сумма чисел делится на 10

1) x ∈ (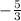, 1)

2) x ∈  (-∞, 2] U [4, +∞)

3) x ∈ (-∞, 2) U (3, +∞)

4) x ∈ (-4, 1)

Объяснения:

1) |3x + 1| < 4.

Рассмотрим возможные случаи:

[  3x + 1 < 4, 3x + 1 ≥ 0                    [  x < 1, x ≥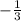

|                                             ⇔      |

[  - (3x + 1) < 4, 3x + 1 < 0                [  x >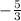 , x <

[  x 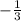∈ [, 1)              [  

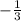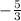|                                                 ⇔      |  x ∈ (, 1)

[  x ∈ (, ) [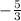  

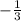2) |2x - 5| ≥ x - 1

|2x - 5| - x ≥ -1

Рассмотрим возможные случаи:

[  2x - 5 - x ≥ - 1, 2x - 5 ≥ 0                    [  x ≥ 4, x ≥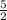

|                                             ⇔             |

[  - (2x - 5) - x ≥ -1, 2x - 5 < 0                 [  x ≤ 2, x <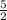

[  x ∈ [4, +∞)                [  

|                           ⇔    |  x ∈  (-∞, 2] U [4, +∞)

[  x ∈ (-∞, 2]                 [  

3) |5 - 2x| > 1

Рассмотрим возможные случаи:

[  5 - 2x > 1, 5 - 2x ≥ 0                    [  x < 2, x ≤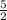

|                                             ⇔      |

[  - (5 - 2x) > 1, 5 - 2x < 0                [  x > 3, x >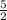

[  x ∈ (-∞, 2)                   [  

|                           ⇔      |  x ∈ (-∞, 2) U (3, +∞)

[  x ∈ (3, +∞)                  [          

4) |x| + |x + 3| < 5

Рассмотрим возможные случаи:

[  x + x + 3 < 5, x ≥0, x + 3 ≥ 0                   [  x < 1, x ≥ 0, x ≥ -3

[  -x + x + 3 < 5, x < 0, x + 3 ≥ 0                 [  x ∈ R, x < 0, x ≥ -3

|                                                            ⇔  |

[  x - (x + 3) < 5, x ≥ 0, x + 3 < 0                 [  x ∈ R, x ≥ 0, x < -3

[  -x - (x+3) < 5, x <0, x + 3 < 0                   [  x > -4, x < 0, x < -3

[  x < 1, x ∈ [0, +∞)                    [  x ∈ [0, 1)               [

[  x ∈ R, x ∈ [-3,0)                     [  x ∈ [-3, 0)             [

|                                          ⇔  |                          ⇔ |  x ∈ (-4, 1)

[  x ∈ R, x ∈ ∅                           [  x ∈ ∅                    [

[  x > -4, x ∈ (-∞, 3)                   [  x ∈ (-4, -3)             [