Алгебра: решить контрольную по производной

решить контрольную по производной

Показать ответ

Ответ:

лоллрр

05.03.2021 13:50

Объяснение:

из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции

1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз

2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз

3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .

теперь проделаем все это с нашей функцией

$\displaystyle y= \frac{1}{4} cos\bigg (\frac{x}{2} +\frac{\pi}{4} \bigg )$

начнем с простого

1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу

2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза

3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду

$\displaystyle f(kx+b)=f\bigg(k\bigg (x+\frac{b}{k} \bigg )\bigg )\\\\y=\frac{1}{4} cos \bigg(\frac{x}{2}+\frac{\pi}{4} \bigg ) =\frac{1}{4} cos\bigg (\frac{1}{2} \bigg (x+\frac{\pi}{2} \bigg )\bigg )$

таким образом у нас будет сдвиг (параллельный перенос) графика

у = cos(x) вдоль оси оx на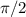 $\displaystyle \pi/2$ единиц влево

ну и вот что должно получиться.

Какие преобразования нужно выполнить над синусоидой y=cosx, чтобы построить график функции

0,0(0 оценок)

Ответ:

Fizruk115

15.07.2021 15:40

Объяснение:

у = sin(x)

Область определения: D(f) = (-∞; +∞) или D(f)∈RОбласть значения: E(f) = [-1; 1]Нули функций: x₀ = πn, n∈ZЧетность функций: sin(-x) = -sin(x) - нечетнаяПериод функций: sin(x+T) = sin(x) ⇒ T = 2πПромежутки монотонности:

y = sin(x)↑ на [-π/2 + 2πn; π/2 + 2πn], n∈Z

y = sin(x)↓ на [π/2 + 2πn; 3π/2 + 2πn], n∈Z

Промежутки знакомо постоянства:

y>0 при x∈(0 + 2πn; π + 2πn), n∈Z

y<0 при x∈(π + 2πn; 2π + 2πn), n∈Z

Наибольшее и наименьшее:

y = 1 - наибольшее при x = π/2 + 2πn,n∈Z;

y = -1 - наименьшее при x = − π/2 + 2πn,n∈Z;

Обратимость: y = arcsin(x) на [- π/2; π/2]Ограниченность: Ограничена сверху и снизуПроизводная: y = (sin(x))' = cos(x)График: (показано внизу)↓
Постройте график функции с подробнейшим пошаговым объяснением. Очень подробно опишите свойства этой