1. Решим квадратное уравнение: . Т. к. дискриминант равен нулю, то корень здесь один: . Парабола касается оси Ox в точке (1;0), а так как коэффициент при иксе в квадрате положительный, значит, ветви параболы направлены вверх. Из этого следует, что y>0 при x∈(-∞; 1)∪(1; +∞), а при x=1 функция равна нулю
2. Область определения функции -- это x∈[0; +∞). Т. к. квадратный корень из числа всегда равен неотрицательному числу, к которому к тому же прибавляется два (в данной функции), то на всей области определения функция положительна: y>0 при x∈[0; +∞).
3. Область определения функции -- это x∈[-2; +∞). Функция равна нулю при x=-2, а на остальной области определения положительна: y>0 при x∈(-2; +∞).
По определению среднее арифметическое равно общей сумме членов деленное на их общее количество: откуда сумма n первых членов арифметической последовательности равна в частности отсюда второй член последовательности равен разность арифметической прогрессии равна значит искомая арифметическая прогрессия это арифметическая прогрессия с первым членов 2, и разностью арифметической прогрессии 4 (2, 6, 10, 14, 18, .....) ---------- /////////// маленькая проверочка схождения с формулой суммы членов прогрессии ////////// ответ: арифмитичесская прогрессия с первым членом 2 и разностью прогрессии 4
1. Решим квадратное уравнение: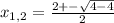
. Т. к. дискриминант равен нулю, то корень здесь один: 
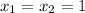. Парабола касается оси Ox в точке (1;0), а так как коэффициент при иксе в квадрате положительный, значит, ветви параболы направлены вверх. Из этого следует, что y>0 при x∈(-∞; 1)∪(1; +∞), а при x=1 функция равна нулю
2. Область определения функции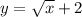
-- это x∈[0; +∞). Т. к. квадратный корень из числа всегда равен неотрицательному числу, к которому к тому же прибавляется два (в данной функции), то на всей области определения функция положительна: y>0 при x∈[0; +∞).
3. Область определения функции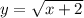
-- это x∈[-2; +∞). Функция равна нулю при x=-2, а на остальной области определения положительна: y>0 при x∈(-2; +∞).
откуда сумма n первых членов арифметической последовательности равна
в частности
отсюда второй член последовательности равен
разность арифметической прогрессии равна
значит искомая арифметическая прогрессия это арифметическая прогрессия с первым членов 2, и разностью арифметической прогрессии 4
(2, 6, 10, 14, 18, .....)
----------
///////////
маленькая проверочка схождения с формулой суммы членов прогрессии
//////////
ответ: арифмитичесская прогрессия с первым членом 2 и разностью прогрессии 4