Наименьшее значение
Объяснение:
x + 2y - 1 = 0 ⇔ 2y = 1 - x ⇔
Введем функцию и найдем её частные производные:
⇒ 3 - y = -4y - 2
3 - y = -4y - 2
3y = -5|:3
⇒
Пусть координаты точки
Минимум функции достигается при
Проверим принадлежит ли точка M прямой
Точка не принадлежит прямой так как
x + 2y - 1 = 0 ⇒ x = 1 - 2y
Введем функцию при этом x выразим через y так данная точка лежит на прямой x + 2y - 1 = 0 и на графике функции
Точка минимума функции которая принадлежит графику x + 2y - 1 = 0 это точка A с координатами
В этой задаче удобно обозначить половину времени через t , тогда всё время будет 2t .
Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 16 км/ч , значит протяжённость первой половины пути :
Вторую половину времени шёл пешком со скоростью 8 км/ч , значит протяжённость второй половины пути равна :
Следовательно , весь путь равен :
Средняя скорость вычисляется по формуле , где S - весь пройденный путь , а t - всё время , за которое этот путь пройден .
Значит :
км/ч - средняя скорость
Наименьшее значение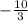
Объяснение:
x + 2y - 1 = 0 ⇔ 2y = 1 - x ⇔
Введем функцию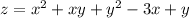 и найдем её частные производные:
и найдем её частные производные:
3 - y = -4y - 2
3y = -5|:3
Пусть координаты точки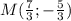
Минимум функции достигается при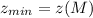
Проверим принадлежит ли точка M прямой
Точка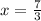 не принадлежит прямой
не принадлежит прямой  так как
так как 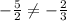
x + 2y - 1 = 0 ⇒ x = 1 - 2y
Введем функцию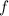 при этом x выразим через y так данная точка лежит на прямой x + 2y - 1 = 0 и на графике функции
при этом x выразим через y так данная точка лежит на прямой x + 2y - 1 = 0 и на графике функции 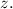
Точка минимума функции которая принадлежит графику x + 2y - 1 = 0 это точка A с координатами
которая принадлежит графику x + 2y - 1 = 0 это точка A с координатами 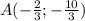
Наименьшее значение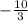
В этой задаче удобно обозначить половину времени через t , тогда всё время будет 2t .
Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 16 км/ч , значит протяжённость первой половины пути :
Вторую половину времени шёл пешком со скоростью 8 км/ч , значит протяжённость второй половины пути равна :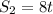
Следовательно , весь путь равен :
Средняя скорость вычисляется по формуле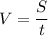 , где S - весь пройденный путь , а t - всё время , за которое этот путь пройден .
, где S - весь пройденный путь , а t - всё время , за которое этот путь пройден .
Значит :