решить алгебру за 10 класс номер 50.2 найдите область определения производной функции y=f(x)

Показать ответ

Ответ:

azalia2003love

19.06.2022 21:20

Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?

При решении данной задачи лучше нарисовать дугу и делать на ней необходимые пометки (рисунок в приложении).

ответ: 9

2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.

Длину ширины MN нужно искать через формулу длины окружности. Так как MN - это полуокружность, то её длина равна πR.

\begin{gathered}\displaystyle \tt \pi R=5,2\\\displaystyle \tt 3,14\cdot R=5,2\\\displaystyle \tt R=5,1\div3,14 \displaystyle \tt MN=2\cdot\frac{520}{314}displaystyle \tt MN=\frac{520}{157}displaystyle \tt MN\approx3,31\end{gathered}

πR=5,2

3,14⋅R=5,2

R=5,1÷3,14

MN=2⋅

314

520

MN=

157

520

MN≈3,31

ответ: 3,3

3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. ответ округлите до целых.

Участок внутри теплицы - прямоугольник, площадь которого равна MN*NP.

\displaystyle \tt S=\frac{520}{157}\cdot4,5=\frac{2340}{157}\approx14,9\approx15S=

157

520

⋅4,5=

157

2340

≈14,9≈15

ответ: 15

0,0(0 оценок)

Ответ:

KOSHAPLAY27082007

28.08.2020 07:32

Объяснение:

Когда основания одинаковые, то вот что с умножением и делением:

а² * а³ =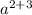 $a^{2+3}$ (например)

а³ : а² =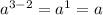 $a^{3-2} = a^{1} = a$ (например)

Когда показатели одинаковые, то вот:

а² + б² = (а + б)²

а² - б² = (а - б)²

а² : б² = (а : б)²

а² * б² = (а * б)²

Когда минус:

-а² = -(а * а)

(-а)² = (-а * -а)² (если показатель чётный, то на выходе будет положительное число, если не четный, то отрицательное)

Несколько степеней:

(а²)³ =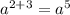 $a^{2+3} = a^{5}$

1. а)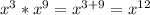 $x^{3} * x^{9} = x^{3+9} = x^{12}$

б)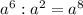 $a^{6} : a^{2} = a^{8}$

в)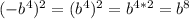 $(-b^{4} )^{2} = (b^{4} )^{2} = b^{4 * 2} = b^{8}$

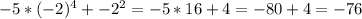
2. $-5 * (-2)^{4} + -2^{2} = -5 * 16 + 4 = -80 + 4 = -76$

3. а)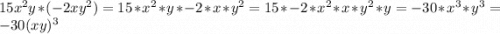 $15x^{2}y * (-2xy^{2}) = 15 * x^{2} * y * -2 * x * y^{2} = 15 * -2 * x^{2} * x * y^{2} * y = -30 * x^{3} * y^{3} = -30(xy)^{3}$

б)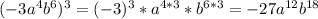 $(-3a^{4}b^{6})^{3} = (-3)^{3} * a^{4*3} * b^{6*3} = -27a^{12}b^{18}$

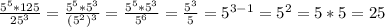
4. $\frac{5^{5} * 125}{25^{3}} = \frac{5^{5} * 5^{3} }{(5^{2})^{3} } = \frac{5^{5} * 5^{3} }{5^{6} } = \frac{5^{3} }{5} = 5^{3-1} = 5^{2} = 5 * 5 = 25$