Это тождество Эйлера, являющееся частным случаем формулы Эйлера при .
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма (алгебра);
2) отношение длины окружности к ее диаметру (геометрия);
3) мнимую единицу (комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".
Это тождество Эйлера, являющееся частным случаем формулы Эйлера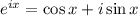 при
при  .
.
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма (алгебра);
(алгебра);
2) отношение длины окружности к ее диаметру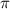 (геометрия);
(геометрия);
3) мнимую единицу (комплексные числа);
(комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".
знаменатели дроби слева и справа одинаковые, на них можно дробь сократить,
но при этом надо учесть ОДЗ - они не могут быть равны 0;
х²-9=х²-3²=(х-3)(х+3) не равно 0,
значит,
ОДЗ х не равно -3 и х не равно +3;
осталось приравнять числители и найти корни
х²=12-х;
х²+х-12=0;
по т Виета
х1+х2=-1;
х1·х2=-12;
решается такое устно
х1=-4;
х2=3 по ОДЗ не подходит
5/(x - 3) - 8/x=3 домножим все на x(x-3) неравное 0
получаем
5x - 8(x -3)=3x(x-3)
5x - 8x+24=3x^2 - 9x
- 3x+24 - 3x^2 +9x=0
- 3x^2 +6x +24=0
x^2 - 2x-8=0
получили квадратное уравнение, решаем через дискриминант
D=4+4*8=36 >0, 2 корня
x1=(2+6)/2=4
x2=(2 - 6)/2= - 2
Из А в В ехал x км/ч. Затратил 48/x ч. Обратно ехал (x+4) км/ч, затратил 40/(x+4) ч, что на 1 ч меньше, то есть
Второй корень не подходит по смыслу. Значит, из А в В велосипедист ехал со скоростью 16 км/ч.