В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение:
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части:
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень
1. найдем область допустимых значений: х ∈ {-4, -1 - корень из 3} ∪ {-1 + корень из 3, +∞}
2. преобразуем неравенство: для 0 < a < 1 выражение log a (x) > log a (y) равно x < y, соответственно log 1/6 (x+4) > log 1/6 (x^2 + 2x - 2) = x + 4 < x^2 + 2x - 2
3. переместим выражение в левую часть и изменим его знак: x + 4 - x^2 - 2x + 2 < 0
4. приведем подобные члены и вычислим сумму: -x + 6 - x^2 < 0
5. поменяем порядок слагаемых/множителей переместительным законом: -x^2 - x + 6 < 0
6. запишем - x в виде разности: -x^2 + 2x - 3x + 6 < 0
7. вынесем за скобки общий множитель -x и -3: -x*(x - 2) - 3*(x - 2) < 0
8. вынесем за скобки общий множитель -(х - 2): -(х - 2)*(х + 3) < 0
9. сменим знаки обеих частей неравенства и поменяем знак неравенства на противоположный: (х -2)*(х + 3) > 0
10. рассмотрим все возможные случаи: возможны два, когда произведение a*b может быть > 0: под знаком системы a > 0 и b > 0 или a < 0 и b < 0, соответственно
11. решим систему неравенства относительно х:
12. найдем пересечения двух систем:
x ∈ {2, +∞}
x ∈ {-∞, -3}
13. найдем объединение:
x ∈ {-∞, -3} ∪ {2, +∞}, х ∈ {-4, -1 - корень из 3} ∪ {-1 + корень из 3, +∞}
14. найдем пересечение множества решений и области допустимых значений, и получим ответ
В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: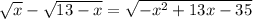
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: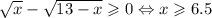
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень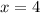
1. найдем область допустимых значений: х ∈ {-4, -1 - корень из 3} ∪ {-1 + корень из 3, +∞}
2. преобразуем неравенство: для 0 < a < 1 выражение log a (x) > log a (y) равно x < y, соответственно log 1/6 (x+4) > log 1/6 (x^2 + 2x - 2) = x + 4 < x^2 + 2x - 2
3. переместим выражение в левую часть и изменим его знак: x + 4 - x^2 - 2x + 2 < 0
4. приведем подобные члены и вычислим сумму: -x + 6 - x^2 < 0
5. поменяем порядок слагаемых/множителей переместительным законом: -x^2 - x + 6 < 0
6. запишем - x в виде разности: -x^2 + 2x - 3x + 6 < 0
7. вынесем за скобки общий множитель -x и -3: -x*(x - 2) - 3*(x - 2) < 0
8. вынесем за скобки общий множитель -(х - 2): -(х - 2)*(х + 3) < 0
9. сменим знаки обеих частей неравенства и поменяем знак неравенства на противоположный: (х -2)*(х + 3) > 0
10. рассмотрим все возможные случаи: возможны два, когда произведение a*b может быть > 0: под знаком системы a > 0 и b > 0 или a < 0 и b < 0, соответственно
11. решим систему неравенства относительно х:
12. найдем пересечения двух систем:
x ∈ {2, +∞}
x ∈ {-∞, -3}
13. найдем объединение:
x ∈ {-∞, -3} ∪ {2, +∞}, х ∈ {-4, -1 - корень из 3} ∪ {-1 + корень из 3, +∞}
14. найдем пересечение множества решений и области допустимых значений, и получим ответ