Поэтому указать промежуток значительно проще чем его решить. Вот смотри само (х²+1) есть уравнение где всегда больше или равно нулю, но так как область определения х≠0 (то есть в знаменателе стоит х, если вместо него подставить нуль, то получиться, что мы делим на нуль, что категорично нельзя делать, на нуль нельзя делить). Выходит, что х принимает любое значение как отрицательное, так и положительное, конечно кроме нуля. Теперь допускаем: 1) Рассмотрим первое слагаемое: мы сказали что (х²+1)≥0 при любом х, тогда пусть х (то что в знаменателе) будет положительное число. Положительное делим на положительное = положительное. рассмотрим второе слагаемое: положительное делим на положительное = положительное. В итоге, положительное + положительное = положительное, а у нас равно -2,5, то есть отрицательное. Значит при х>0 уравнение не выходит.
2) Рассмотрим первое слагаемое: также числитель ≥0, ну а х теперь возьмем <0, то есть отрицательное. положительное делим на отрицательное = отрицательное. Рассмотрим второе слагаемое: отрицательное делим на положительное = отрицательное. Имеем отрицательное минус отрицательное = отрицательное то есть нашему -2,5.
Выходит что лишь в промежутке (-бескон; 0) (где нуль исключаем ) находиться решение нашего уравнения. Вот так
S полн. пов =2430
Объяснение:
Sполн. пов=Sбок.пов+2*Sосн
Sбок.пов=Росн*Н, Н - высота призмы
Sосн=S трапеции =(a+b)*h/2, h - высота трапеции
1. ABCD - трапеция
AB=25, BC=16, CD=17, AD=44.
дополнительные построения:
BM_|_AD, CN_|_AD, BC=MN=16
пусть DN=x, тогда
AD=AM+MN+ND
44=AM+16+x,
AM=44-(16+x), AM=28-x
2. рассмотрим прямоугольный треугольник АМВ:
∠M=90°
гипотенуза АВ=25
катет АМ=28-х
катет ВМ найти по теореме Пифагора:
AM²=AB²-BM²
AM²=25²-(28-x)²
AM²=-x²+56x-159
3. рассмотрим прямоугольный треугольник DNC:
гипотенуза CD=17
катет DN=x
катет CN найти по теореме Пифагора:
CN²=CD²-DN²
CN²=17²-x²
4. BM=CN, =>
уравнение: -х²+56x-159=17²-x²
56x=448
x=8
CN²=17²-8², CN=15
5.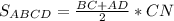
6. S полн. пов=(25+16+17+44)*15+2*450=2430
Вот смотри само (х²+1) есть уравнение где всегда больше или равно нулю, но так как область определения х≠0 (то есть в знаменателе стоит х, если вместо него подставить нуль, то получиться, что мы делим на нуль, что категорично нельзя делать, на нуль нельзя делить).
Выходит, что х принимает любое значение как отрицательное, так и положительное, конечно кроме нуля.
Теперь допускаем:
1) Рассмотрим первое слагаемое:
мы сказали что (х²+1)≥0 при любом х, тогда пусть х (то что в знаменателе) будет положительное число. Положительное делим на положительное = положительное.
рассмотрим второе слагаемое: положительное делим на положительное = положительное.
В итоге, положительное + положительное = положительное, а у нас равно -2,5, то есть отрицательное.
Значит при х>0 уравнение не выходит.
2) Рассмотрим первое слагаемое:
также числитель ≥0, ну а х теперь возьмем <0, то есть отрицательное.
положительное делим на отрицательное = отрицательное.
Рассмотрим второе слагаемое:
отрицательное делим на положительное = отрицательное.
Имеем отрицательное минус отрицательное = отрицательное то есть нашему -2,5.
Выходит что лишь в промежутке (-бескон; 0) (где нуль исключаем ) находиться решение нашего уравнения.
Вот так