Пусть второй каменщик сделает работу за х часов, а первый - за у часов. Тогда по условию, x - y = 6. Производительность труда первого каменщика равна , а производительность труда второго каменщика равна . Зная, что они за 2 часа выложат половину стены, составим и решим систему уравнений
Умножим левую и правую части уравнения на 2x(x-6) ≠ 0
По теореме Виета
— не удовлетворяет условию;
часов потребуется выложить стену второму каменщику;
Пусть второй каменщик сделает работу за х часов, а первый - за у часов. Тогда по условию, x - y = 6. Производительность труда первого каменщика равна , а производительность труда второго каменщика равна
, а производительность труда второго каменщика равна  . Зная, что они за 2 часа выложат половину стены, составим и решим систему уравнений
. Зная, что они за 2 часа выложат половину стены, составим и решим систему уравнений
Умножим левую и правую части уравнения на 2x(x-6) ≠ 0
По теореме Виета
Первому каменщику потребуется 12 - 6 = 6 часов.
ответ: 6 часов и 12 часов.
№1
находим корни числителя и знаменателя:
(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.
Используем метод интервалов:
точки (-2) и 5 - выколотые.
+ - + + - +
-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x
ответ:![x\in [-3;-2)\cup (5;8] \cup \{ 3 \}](/tpl/images/0999/4162/b28f6.png)
№2
точки (-1) и 4 - выколотые
+ + - +
------[-6]------(-1)------(4)------->x
ответ: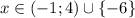
№3
замена:
получим:
обратная замена:
+ - + - +
-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x
ответ:![x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)](/tpl/images/0999/4162/cc812.png)