Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)
https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48
Объяснение:
https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48https://edu.gounn.ru/journal-api-online_lessons-action?action=setStudentDateStart&isExtDay=0&onlineLessonId=48
ответ: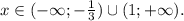
Объяснение:
-3x² + 2x +1 < 0;
3x² - 2x - 1 > 0;
Дискриминант равен 2²+4*1*3 = 4+12 = 16.
Корни трехчлена равны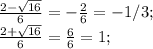
Значит 3x² - 2x - 1 = (3x+1)(x-1) > 0;
Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)