Разложить на множители в №1-№3
№1. 15а - 5ау
№2. 12р3к2 – 6р4к + 2р6 к5
№3. a2b2 - ab+abк - к
№4. Раскрыть скобки, привести подобные слагаемые:
(m+n) (m-n) + 2(m2 – n2)
№5. Представьте в виде квадрата двучлена: 1 + 6а + 9a2 .
№6. Решите уравнение: 18у – 2у3 =0.
№7. У выражение:
(5х+3)2 –(5х+2)∙ ( 5х – 2 ).

Показать ответ

Ответ:

kskkksjsjsj

28.10.2020 23:17

а и а^2 здесь можно представить в виде любого числа. Попробуем это сделать. Для начала, выясним, при каких значениях а=а^2. Естественно, условие выполняется при значении 0, также ему удовлетворяют значения 1 и -1. Возаедём их для ясности в квадрат и получим:

1×1=1

-1×(-1)=1. Следовательно, 1=1 и а =а^2.

Теперь выясним, почему же при других значениях а<а^2. Подставим нппример значение 2. Тогда получим, что 2^2=4 и 2<4. А если вдруг число будет отрицательным? Попробуем подставить и получим:

-2^2=-2×(-2)=4. Соответственно, получим такое неравенство:

2<-4. Проведя такое доказательство, можно прийти к выводу, что а<=а^2.

0,0(0 оценок)

Ответ:

valeriarodriger

07.07.2020 04:37

Декартовы координаты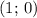 $(1;\,0)$ на числовой окружности имеет угол .

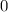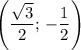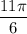Декартовы координаты $\left(\dfrac{\sqrt{3}}{2};\,-\dfrac{1}{2}\right)$ на числовой окружности имеет угол $\dfrac{11\pi}{6}$ .

Учитывая, что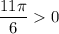 $\dfrac{11\pi}{6}0$ и то, что поворот против часовой стрелки является движением в положительную сторону на числовой окружности, находим угол поворота:

$\dfrac{11\pi}{6}-0=\dfrac{11\pi}{6}$

Но, так как длина одного полного оборота по числовой окружности равна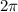 $2\pi$ , то, пройдя еще некоторое количество кругов в ту же сторону, мы попадем снова в исходную точку. Поэтому, все искомые углы определяются формулой: