Расстояние между двумя пристанями равно 113,4 км. Из них одновременно навстречу друг другу вышли две лодки, скорости которых в стоячей воде равны. Через 2,1 ч. лодки встретились. Скорость течения реки равна 3 км/ч. Скорость лодки в стоячей воде равна км/ч.
Сколько километров до места встречи пройдёт лодка, плывущая по течению? км. Сколько километров до места встречи пройдёт лодка, плывущая против течения? км
Известно, что для того, чтобы дробь имела смысл, знаменатель её должен быть больше нуля. Поэтому искать значения х следует через неравенство:
х² - 12х + 20 > 0
Приравнять к нулю и решить как квадратное уравнение:
D=b²-4ac =144 - 80 = 64 √D= 8
х₁=(-b-√D)/2a
х₁=(12-8)/2
х₁=4/2
х₁=2;
х₂=(-b+√D)/2a
х₂=(12+8)/2
х₂=20/2
х₂=10.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 2 и х= 10, отмечаем эти точки схематично, смотрим на график.
На графике ясно видно, что х может принимать любые значения, кроме х=2 и х=10, знаменатель при таких значениях х равен нулю, что недопустимо.
Решение уравнения: х∈R (все значения х); х≠2; х≠10 (кроме 2 и 10).
В решении.
Объяснение:
Известно, что для того, чтобы дробь имела смысл, знаменатель её должен быть больше нуля. Поэтому искать значения х следует через неравенство:
х² - 12х + 20 > 0
Приравнять к нулю и решить как квадратное уравнение:
D=b²-4ac =144 - 80 = 64 √D= 8
х₁=(-b-√D)/2a
х₁=(12-8)/2
х₁=4/2
х₁=2;
х₂=(-b+√D)/2a
х₂=(12+8)/2
х₂=20/2
х₂=10.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 2 и х= 10, отмечаем эти точки схематично, смотрим на график.
На графике ясно видно, что х может принимать любые значения, кроме х=2 и х=10, знаменатель при таких значениях х равен нулю, что недопустимо.
Решение уравнения: х∈R (все значения х); х≠2; х≠10 (кроме 2 и 10).
Відповідь:
1.
f(2)=8
f(-1)= - 2,5
нулі: f(0)=0
2. D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3) в завданні
5)х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞)
6)p=8 q=22
Пояснення:
1)f(2)=1/2*2²+3*2=2+6=8;
f(-1)=1/2*(-1)²+3*(-1)=0,5-3=-2,5
нулі х=0; f(0)=1/2*0+3*0=0 (при у=0 х=0)
2.область визначення функції: оскільки це дріб, то знаменник не може бути рівний 0
х²-10х+24≠0 D=(-10)²-4*1*24=100-96=4
x₁≠(10-2)/2≠4
x²≠(10+2)/2=6
Відповідь: D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3. Побудувати графік функції:
це парабола , вітки направлені догори
Знайдемо точки перетину з вісью ОХ
x²+2x-3=0 по теоремі Вієта х1= - 3 , x2= 1.
координати вершини: хв=-2/2=-1, ув=(-1)²+2*(-1)-3=-4 (-1;-4)
при х=0, у=-3
графік перемалюєш з картинки
1)f(x)>0 при х ∈ (-∞; -3) ∪ (1;+∞)
f(x)<0 при х ∈ (-3; 1)
2)Е(f) : y ∈ (-5;+∞)
3) функція зростає при х ∈ [-1; +∞)
4.
маєш в файлі синя- перша, червона -друга( побудуй функцію онлайн і перемалюй таблицю точок)
5. Область визначення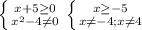
Відповідь: ОДЗ: х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞).
6) хв=-4 ; -4=-p/2*1;p=8
ув=6
6=(-4)²+8(-4)+q;
q=6-16+32=22
f(x)=x²+8x+22
p=8 q=22