Произведение положительного числа на положительное является положительным, т.е
3*b>0 при b>0
Сумма двух положительных будет положительна, т.е a+3*b>0, если а>0 и b>0
Значит и произведение 2а*(а+3b) положительное Раскрываем скобки получаем
Т.к а>0 и b>0, то a*b>0,
для любых а.
Сумма двух положительных чисел, будет положительным числом, получаем что
при условии что a*b>0 (это возможно при a>0 и b>0, или a<0 и b<0)
Строго говоря этим мы доказали, не только что 2а(а+3b)>0 не только при а и b>0, но и при а и b<0. Т.е. чтобы выполнялось неравенство необходимо и достаточно чтобы a и b были одного знака.
а>0,b>0, тогда и
2а > 0
и
(а + 3b) > 0
Произведение двух положительных чисел -также является положительным числом, поэтому
2а ·(а + 3b) > 0
3*b>0 при b>0
Сумма двух положительных будет положительна, т.е a+3*b>0, если а>0 и b>0
Значит и произведение 2а*(а+3b) положительное Раскрываем скобки получаем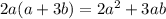
Т.к а>0 и b>0, то a*b>0,
Сумма двух положительных чисел, будет положительным числом, получаем что
Строго говоря этим мы доказали, не только что 2а(а+3b)>0 не только при а и b>0, но и при а и b<0. Т.е. чтобы выполнялось неравенство необходимо и достаточно чтобы a и b были одного знака.