Прямоугольный участок размером 48x62 покрывается плитками. можно ли покрыть этот участок ровными плитками 4х3? 6х14? обоснуйте свой ответ. если да, то сколько плиток для этого потребуется?

очень легко нужно просто это все и всае вчсе да это очень легко может ты просто будешь да Действие развивается вокруг Элоизы «Элли» Тернер — амбициозной девушки, которая мечтает стать профессиональным модельером. Для осуществления заветного желания она отправляется в Лондон, чтобы поступить в колледж и построить успешную карьеру, но проводит будни в одиночестве. Лишь ночью жизнь Элоизы начинает играть бурными красками и наполняться интересными событиями, поскольку во сне она таинственным образом переносится в прошлое — в 1960-е годы. Именно здесь Элли встречает своего кумира — очаровательную певицу Сэнди, которая делает первые шаги в мире гламура, роскоши и лжи.

1)  Множество точек, удовлетворяющих неравенству   ,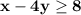

 ,   лежат ниже прямой     .

Множество точек, удовлетворяющих неравенству  

лежат внутри окружности с центром в точке ( 1 : 0) , радиуса  R=2 .

2) Множество решений системы неравенств изображено на рисунке.

Область заштрихована . Это полоса между прямыми х= -2  и  х=2 , расположенная выше прямой у=3 . Сами прямые в область не входят, так как неравенства имеют строгие знаки .

 

3)  Фигура, изображённая на рисунке, может быть задана с системы неравенств   .      

Неравенство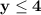    описывает множество точек, лежащих ниже прямой у=4 .

Неравенство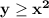    описывает множество точек, расположенных внутри параболы  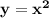 .  Это можно определить, если рассматривать точку , которая находится внутри параболы , например, точка (1;2) , и точку с той же абсциссой х=1 , лежащую на параболе, имеющую ординату  у=1²=1 . Сравним ординаты этих точек: 2>1 . Значит ординаты точек, находящихся внутри параболы, больше , чем ординаты точек, лежащих на параболе . Отсюда и получаем  у≥х²  .