Прямая СВ проходит через начало координат и точку А (3; 1). Графиком какой функции является эта прямая?
А) у =3х +1
Б) у = 3х
В) у = 1/3 х
2.Найдите точку пересечения графика функции у = 0,5х + 4 с осями координат
1) А (0; 4), В (8; 0)
2) А (0; 4), В (-8; 0)
3) А (4; 0), В (0; 8)​

чтобы решить уравнение нужно привести всё к общему знаменателю

  х        7           8

___  -   =

х-2      х + 2    х² - 4

нижний знаменатель х² - 4 можно разложить по формуле разности квадрата. вы её наверняка проходили.

получится (х-2)(х+2)

всё уравнение имеет вид

  х        7           8

___  -   =

х-2      х + 2    (х-2)(х+2)

ну а теперь домножаем до одного знаменателя. в первом столбике умножим на (х+2), во втором на (х-2), а третий так и оставим.

получится:

х(х+2) - 7(х-2) - 8

      =  0;

(х-2)(х+2)

когда раскроем скобки получится:

х² + 2х - 7х + 14 - 8

  =  0;

(х-2)(х+2)

сверху получится х² - 5х + 6 = 0

находим через дискриминант. D = b² - 4ac;

D = 25 - 4*6 = 25-24 = 1;

х₁= -b + √D

      =  5 + 1 

           2a           2

x₁ = 3;

х₂ = 5-1

       ___   = 2

         2

всё уравнение имеет вид

(x-2)(x-3)

=  0;

(х-2)(х+2)

сократив дробь получим

х-3

___   = 0;

х + 2 

т.к. делить на ноль нельзя, то х+2 ≠0

х ≠ -2

ответ: х∋(-∞;-2)(-2;+∞)

на самом деле это несложное уравнение, просто я пыталась как можно больше объяснить свои действия :)

по формуле приведения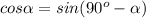

так как 18+36=54, то

т.е.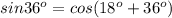 (1)

по формуле синуса двойного угла(аргумента)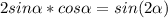

(2)

по формуле косинуса суммы :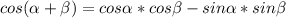

(3)

Подставив (2) и (3) в (1) получим

(4)

используя формулы синуса двойного угла (выше упоминалась) и косинуса двойного угла

имеем что

(5)

Подставляя (5) в (4), упращая и сокращая обе части равенства на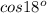

(6)

Получили квадратное уравнение относительно sin 18

так как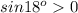 , как синус острого угла (т.е. угла большег 0 градусов и меньшего 90 градусов)

Как-то так*