Если k > -5
Если k < -5
Что бы в (k, -5) ( или (-5, k)) содержалось четыре целочисленных решения, достаточно, что бы
Целочисленными значениями параметра k, при которых имеется четыре целочисленных решения, будут: -10, 0
Если k > -5
Если k < -5
Что бы в (k, -5) ( или (-5, k)) содержалось четыре целочисленных решения, достаточно, что бы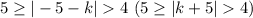
Целочисленными значениями параметра k, при которых имеется четыре целочисленных решения, будут: -10, 0