Представьте в виде многочлена выражение: 7) (9m+⅓n)²
9) (x³-x2)²
10) (p²+p⁴)²
11) (-11b+2a⁵)²
12) (-8-4c)²
13) 1⅔p+2⅖q)²
14) (12xy²-x²y)²
15) (4a⁶+3a⁴b³)²
Упростить выражение:
5) b(b-3)-(b-4)²
6) (12a-b)²-(9a-b)(16a+2b)
7) x(2x-9)²-2x(15+x)²
8) (x+2)²-(x-3)(x+3)
9) (7a-5b)(7a+5b)-(4a+7b)²
10) (y-2)(y+3)-(y-1)²+(5-y)(y+5)
Решите уравнение:
2) (2x-3)²+(3-4x)(x+5)=82
3) x(x-3)(4-x)=16-x(x-3,5)²
4) (4x-1)²-(2x-3)(6x+5)=4(x-2)²+16x
5) (x-1)(x+1)=2(x-5)²-x(x-3)
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство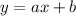
. Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить 
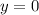. Тогда получим, что 
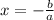, значит пересечение с осью x происходит в точке 
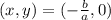. Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.
Раскрывать модули будем постепенно, снаружи, как будто снимая листья с кочана капусты)))
Помним о важном правиле:
|x| =x, если x>=0
|x|=-x, если x<0
Снимаем первый модуль и действуем согласно вышеупомянутому правилу:
{|2^x+x-2|-1 >2^x-x-1
{|2^x+x-2|-1> -2^x+x+1
Переносим "-1" из левой части в правую:
{|2^x+x-2| > 2^x-x
{|2^x+x-2| > -2^x+x+2
2) Снимаем второй модуль и также действуем согласно модульному правилу:
{2^x+x-2>2^x-x {2x-2>0
{2^x+x-2>x-2^x {2*2^x-2>0
{2^x+x-2>-2^x+x+2 {2*2^x-4>0
{2^x+x-2>2^x-x-2 {2x>0
{x>1 {x>1
{2^x>1 {x>0
{2^x>2 {x>1
{x>0 {x>0
Решением неравенства является промежуток (1; + беск.)