1) Сократим числа (в числителе) и (в знаменателе) на . Далее сократим (в числителе) и (в знаменателе) на . В конце сократим (в числителе) и (в знаменателе) на . В итоге получаем:
2) Вынесем в числителе за скобку общий множитель , а затем сократим и в числителе, и в знаменателе на :
3) В числителе представим число в виде . По такой записи сразу понятно, что это формула сокращённого умножения (разность квадратов: ). Раскладываем эту запись.
В знаменателе тоже скрывается формула сокращённого умножения (квадрат разности: ).
Далее сокращаем разложенные на множители формулы.
Но для этого нужно в числителе в 1 скобке поменять местами и и соответственно их знаки. Для этого мы выносим за скобку минус, а в скобке меняем местами числа и их знаки.
Поведем некоторые преобразования. Рассмотрим, в каких пределах может изменяться величина f=(sin x+0.5)². Мы знаем, что синус может меняться в пределах от -1 до 1. Максимальное значение f=2.25 достигается при sin x = 1 При этом значение y будет минимальным и составит 1.25-2.25 = -1. Максимальное значение у можно получить, если вычесть из 1.25 что-то отрицательное или положительное, но как можно меньшей величины. f - это квадрат некоторого выражения и отрицательным он быть не может. Но при sin x=-0.5 получаем f=0 и y=1.25
Решение в разделе "Пошаговое объяснение".
Объяснение:
1) Сократим числа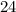 (в числителе) и
(в числителе) и 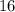 (в знаменателе) на
(в знаменателе) на 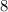 . Далее сократим
. Далее сократим 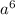 (в числителе) и
(в числителе) и 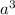 (в знаменателе) на
(в знаменателе) на 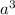 . В конце сократим
. В конце сократим 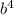 (в числителе) и
(в числителе) и 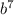 (в знаменателе) на
(в знаменателе) на 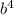 . В итоге получаем:
. В итоге получаем:
2) Вынесем в числителе за скобку общий множитель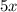 , а затем сократим
, а затем сократим 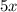 и в числителе, и в знаменателе на
и в числителе, и в знаменателе на 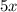 :
:
3) В числителе представим число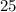 в виде
в виде 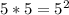 . По такой записи сразу понятно, что это формула сокращённого умножения (разность квадратов:
. По такой записи сразу понятно, что это формула сокращённого умножения (разность квадратов: 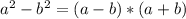 ). Раскладываем эту запись.
). Раскладываем эту запись.
В знаменателе тоже скрывается формула сокращённого умножения (квадрат разности: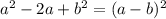 ).
).
Далее сокращаем разложенные на множители формулы.
Но для этого нужно в числителе в 1 скобке поменять местами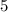 и
и 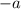 и соответственно их знаки. Для этого мы выносим за скобку минус, а в скобке меняем местами числа и их знаки.
и соответственно их знаки. Для этого мы выносим за скобку минус, а в скобке меняем местами числа и их знаки.
Далее сокращаем и записываем ответ.
Рассмотрим, в каких пределах может изменяться величина f=(sin x+0.5)².
Мы знаем, что синус может меняться в пределах от -1 до 1.
Максимальное значение f=2.25 достигается при sin x = 1
При этом значение y будет минимальным и составит 1.25-2.25 = -1.
Максимальное значение у можно получить, если вычесть из 1.25 что-то отрицательное или положительное, но как можно меньшей величины. f - это квадрат некоторого выражения и отрицательным он быть не может. Но при sin x=-0.5 получаем f=0 и y=1.25
ответ: y ∈ [-1;1.25]