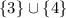Решение подобного биквадратного уравнения сводится к замене вида:
Исходя из области определения корнями будут:
ответ:
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида:
tg 2a = 2tg a / (1 - tg² a).
Нам необходимо знать как минимум тангенс угла. Иы знаем, что
tg a = sin a / cos a
Нам осталось найти лишь синус, косинус равен:
2cos a = -1/4
cos a = -1/8
Синус угла найдём из основнго тригонометрического тождества:
sin² a + cos² a = 1
sin² a = 1 - cos² a
sin² a = 1 - 1/64
sin²a = 63/64
sin a = √63 / 8 или sin a = - √63 / 8
Мы видим, что a - угол второй четверти, где синус положителен. Значит,
sin a = √63/ 8
Найдём отсюда tg a
tg a = √63 / 8 : (-1/8) = -√63
Ну и теперь осталось лишь подставить в исходную формулу получееное значение тангенса:
tg 2a = -2√63 / (1 - 63) = -2√63 / -62 = √63 / 31
1)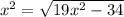
Область определения уравнения:
Возведем обе неотрицательные части в квадрат:
Решение подобного биквадратного уравнения сводится к замене вида: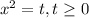
Исходя из области определения корнями будут:
ответ: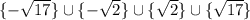
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида: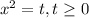
Исходя из области определения корнями будут:
ответ: