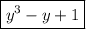Повторение. Решение линейных неравенств с одной переменной Линейные неравенства с одной переменной.
Определение.
Линейным неравенством с одной переменной называют неравенства вида:
ax + b > 0,
ax + b < 0,
ax + b ≥ 0,
ax + b ≤ 0,
где a и b некоторые числа, причем, a ≠ 0.
Алгоритм решения линейных неравенств.
1) Раскрыть скобки.
2) Перенести слагаемые, содержащие переменную влево, а свободные члены, то есть числа вправо, меняя при этом знак слагаемых на противоположный.
3) Привести подобные слагаемые.
4) Разделить обе части неравенство на коэффициент, стоящий перед переменной (если данное число положительное, то знак неравенства не меняется; если число отрицательное, то знак неравенства меняется на противоположный).
5) Перейти к геометрической модели ответа, то есть изобразить решение неравенства в виде числового промежутка.
6) Записать ответ.
Пример.
Реши неравенство:
5 ⋅ (x – 3) > 2x – 3
5x – 15 > 2x – 3
5x – 2x > –3 + 15
3x > 12
3 ⋅ x > 12 |(:3)
x > 4
ответ: (4; +∞).
y=-x^2 Это квадртичная функция
График функции- парабола , ветви направлены вниз, т.к. а меньше нуля.
Это самая простая квадратичная функция (-х)^2 =х^2 (четная степень), значит функция чётная.
У параболы всегда есть вершина.Здесь это А(0;0).Наша парабола касается оси абсцисс в точке А(0;0), проходя через начало координат.
Любая парабола имеет ось симметрии. У нас это прямая х=0(ось ординат)
Чтобы построить график этой функции надо найти координаты точек
У(0)=0 У(-1)=-1
У(1)=-1 У(-2)=-4
У(2)=-4 У(-3)=-9
У(3)=-9
Можно в табличке записать
Х 0 1 2 3 4 -1 -2 -3
У 0 -1 -4 -9 -16 -1 -4 -9
Построй систему координат, а потом по точкам нарисуешь плавно параболу, только не заканчивай ветви на точках, ветви идут в бесконечность, т.к. Х может быть любым. Желаю удачи.
Ну насчет столбиком шутки шутками, а ведь можно делить многочлен на многочлен уголком, только в LaTeX это особо не распишешь. А вот разложить на множители вполне можно.
Сначала займемся числителем:
Здесь часто использовался метод искусственного добавления и вычитания слагаемых для вынесения за скобки общих множителей (в виде скобок). Вот каких - дело опыта, но имея опыт с нахождением корней многочленов высоких степеней, я уже знал, конечно, что в разложении будут присутствовать скобки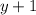 и
и 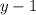 и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.
и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.
Получили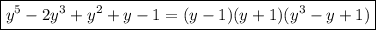
Теперь знаменатель: по известной формуле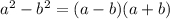
получаем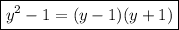
Осталось все это написать вместе и сократить
Сокращать можно только учитывая ограничения
ответ: