Постройте график в п1 линейной функции. по графику определите: а)координаты точек пересечения с осями координат б)значение функции при x=-2; -1; 2 в)значение агрумента если у=-3; 1; 4
Подставим теперь то, как мы представили y под второе выражение. Таким образом, получим уравнение уже с одной неизвестной(x), а не с двумя (x, y), которое будет очень просто решить:
Мы нашли значения x. Теперь можем подставить их либо в первую часть системы уравнений, либо во вторую, здесь нет разницы, допустим, подставим в первую:
(здесь, думаю, можно не расписывать решения при x = 1 и при x = -1, так как у нас x в обоих выражениях в квадрате, а любое число в квадрате, будь то положительное или отрицательное, всегда даст положительное число(т.е. (-1)² = 1 и 1² = 1))
ответ: (-1; 5), (1; 5)
P.S. Не знаю, правильно ли расписано решение, ибо я решила, как сама знаю, пока что. Но ответ точно правильный, надеюсь, хоть как-то, да
Приравнять к нулю и решить как квадратное уравнение:
x²-x-12=0
D=b²-4ac = 1 + 48 = 49 √D= 7
х₁=(-b-√D)/2a
х₁=(1-7)/2
х₁= -6/2
х₁= -3;
х₂=(-b+√D)/2a
х₂=(1+7)/2
х₂=8/2
х₂=4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (график ниже оси Ох) при х∈[-3; 4].
Решение неравенства х∈[-3; 4].
Неравенство нестрогое, скобки квадратные.
b) x² - 16 < 0
Приравнять к нулю и решить как квадратное уравнение:
x² - 16 = 0
x² = 16
х = ±√16
х = ±4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -4 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у < 0 (график ниже оси Ох) при х∈(-4; 4).
Решение с объяснением:
Представим y из первого выражения:
Подставим теперь то, как мы представили y под второе выражение. Таким образом, получим уравнение уже с одной неизвестной(x), а не с двумя (x, y), которое будет очень просто решить:
Мы нашли значения x. Теперь можем подставить их либо в первую часть системы уравнений, либо во вторую, здесь нет разницы, допустим, подставим в первую:
(здесь, думаю, можно не расписывать решения при x = 1 и при x = -1, так как у нас x в обоих выражениях в квадрате, а любое число в квадрате, будь то положительное или отрицательное, всегда даст положительное число(т.е. (-1)² = 1 и 1² = 1))
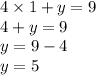
ответ: (-1; 5), (1; 5)P.S. Не знаю, правильно ли расписано решение, ибо я решила, как сама знаю, пока что. Но ответ точно правильный, надеюсь, хоть как-то, да
В решении.
Объяснение:
Розвяжіть нерівність:
а) x²-x-12<= 0.
Приравнять к нулю и решить как квадратное уравнение:
x²-x-12=0
D=b²-4ac = 1 + 48 = 49 √D= 7
х₁=(-b-√D)/2a
х₁=(1-7)/2
х₁= -6/2
х₁= -3;
х₂=(-b+√D)/2a
х₂=(1+7)/2
х₂=8/2
х₂=4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (график ниже оси Ох) при х∈[-3; 4].
Решение неравенства х∈[-3; 4].
Неравенство нестрогое, скобки квадратные.
b) x² - 16 < 0
Приравнять к нулю и решить как квадратное уравнение:
x² - 16 = 0
x² = 16
х = ±√16
х = ±4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -4 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у < 0 (график ниже оси Ох) при х∈(-4; 4).
Решение неравенства х∈(-4; 4).
Неравенство строгое, скобки круглые.