Её можно получить из графика гиперболы путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
Графиком функции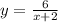 является гипербола.
является гипербола.
Её можно получить из графика гиперболы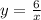 путём сдвига на 2 единицы влево вдоль оси ОХ.
путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
у(наибол)=у(0)=3 , у(наимен)=у(4)=1
На области определения функция убывающая.