Обозначим всю работу по осушению котлован через 1. Пусть х ч и у ч требуется по одиночке на осушение котлована первому и второму насосам соответственно. Тогда производительность каждого насоса есть 1/х котлована за час и 1/у котлована за час соответственно. При разнице в 9 ч получим у-х=9, при одновременной работе получим (1/х + 1/у)*9 = 1.решаем систему уравнений
20(2x+9)=x(9+x)
40x+180=x^2+9x
x^2 -31x -180=0
х1=-5 не удовлетворяет условию
х2=36
Значит 36 ч требуется первому, а 36+9 = 45 ч -второму насосу.
У таких функций графики - кусочно-линейные функции.
Строятся(функции и их графики) так.
1. Определяются все нули у всех модулей и наносятся на числовую прямую
2. На каждом получившемся интервале раскрываются модули и выписывается "нормальная" функция
Всё!
На нашем примере
-3х+6 = 0 -2х-8=0
х=2 х=-4
Нужно рассмотреть 3 интервала
1. х<-4
y = (-3x+6) + (-2x-8) = -5x - 2
2. -4<=x<2
y = (-3x+6) + (2x+8) = -x + 14
3. x>=2
y = (3x-6) + (2x+8) = 5x +2
Ну вот и всё, функция написана в виде кусочно-линейной, на каждом из интервалов строй свой график.
Успехов!
Обозначим всю работу по осушению котлован через 1. Пусть х ч и у ч требуется по одиночке на осушение котлована первому и второму насосам соответственно. Тогда производительность каждого насоса есть 1/х котлована за час и 1/у котлована за час соответственно. При разнице в 9 ч получим у-х=9, при одновременной работе получим (1/х + 1/у)*9 = 1.решаем систему уравнений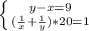
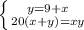
20(2x+9)=x(9+x)
40x+180=x^2+9x
x^2 -31x -180=0
х1=-5 не удовлетворяет условию
х2=36
Значит 36 ч требуется первому, а 36+9 = 45 ч -второму насосу.