Построй график функции y=x и по графику определи координаты точки пересечения графика функции с осью Oy. 1) Заполни таблицу.
2) Используя таблицу, построй график функции и сравни его с данным в шагах решения.
3) Определи координаты точки пересечения с осью Oy.
1) Таблица:
x -1 0 1
y
2) График.
3) Точка пересечения с осью Oy:
( ) ; ( )
В решении.
Объяснение:
Одночлен называется представленным в стандартном виде , если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена, сумму показателей степени переменных называют степенью одночлена.
1) (2х²)³ * х²/4 =
= 8х⁶ * х²/4 =
= 8х⁸/4 = 2х⁸. Стандартный вид. (х в восьмой степени).
2) (-3а⁴)⁵ * а³/27 =
= -243а²⁰ * а³/27 =
= -243а²³/27 = -9а²³. Стандартный вид. (а в 23 степени).
Объяснение:
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна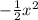
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.