Всех двухэлементных подмножеств пятиэлементного множества М будет штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .
Всех двухэлементных подмножеств пятиэлементного множества М будет штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .
Множество M={ 1 ,2 ,3 ,4 ,5 }
Всех двухэлементных подмножеств пятиэлементного множества М будет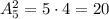
штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .
Всех двухэлементных подмножеств пятиэлементного множества М будет
штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .
(6x-1)²-(3-8x)(3+8x)-(10x+1)²=0
(6x-1)²+(8x-3)(8x+3)-(10x+1)²=0
(36x²-12x+1)+(8x-3)(8x+3)-(100x²+20x+1)=0
(36x²-12x+1)+(64x²-9)-(100x²+20x+1)=0
36x²-12x+1+64x²-9-100x²-20x-1=0
-32x-9=0
-32x=9
32x=-9
x=(-9)÷32
x=-9/32
5(x+2)^2+(2x-1)^2-9(x+3)(x-3)=22
5(x+2)²+(2x-1)²-9(x+3)(x-3)-22=0
5(x²+4x+4)+(4x²-4x+1)-9(x+3)(x-3)-22=0
(5x²+20x+20)+(4x²-4x+1)-(9x+1)-(9x+27)(x-3)-22=0
(5x²+20x+20)+(4x²-4x+1)-(9x²-27x+27x-81)-22=0
(5x²+20x+20)+(4x²-4x+1)-(9x²-81)-22=0
5x²+20x+20+4x²-4x+1-9x²+81-22=0
16x+80=0
16x=-80
x=(-80)÷16
x=-5