Если максимально, то и тоже максимально.
Выражаем из равенства и подставляем в выражение:
Получившееся выражение – квадратичная функция относительно . Известно, что максимум такой функции достигается в вершине, в данном случае – при
Тогда , '
Этим значениям x и y соответствует значение произведения
ответ. 9
ответ 9
просто свой Положительные числа x и y таковы, что x^2+(y^2)/9=6. найдите наибольшее возможное значение выражения">
Если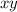 максимально, то и
максимально, то и 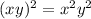 тоже максимально.
тоже максимально.
Выражаем из равенства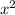 и подставляем в выражение:
и подставляем в выражение:
Получившееся выражение – квадратичная функция относительно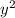 . Известно, что максимум такой функции достигается в вершине, в данном случае – при
. Известно, что максимум такой функции достигается в вершине, в данном случае – при
Тогда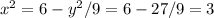 ,
, 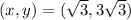 '
'
Этим значениям x и y соответствует значение произведения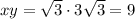
ответ. 9
ответ 9
просто свой Положительные числа x и y таковы, что x^2+(y^2)/9=6. найдите наибольшее возможное значение выражения">