Подробное решение, не из интернета, . так чтобы я поняла.

y=x^2-3x+2

1) Находим точки пересечения графика функции с осью Ох:

     х^2-3x+2=0

     x1=1, x2=2

    (1;0) и (2;0) - искомые точки

2) Находим уравнение касательной к графику функции в точке х=1

    y`(x)=(x^2-3x+2)`=2x-3

    y`(1)=2*1-3=-1   k1=-1

    y(1)=1^2-3*1+2=1-3+2=0

    y=0+(-1)(x-1)=-x+1 -уравнение касательной в точке х=1

3) Находим уравнение касательной к графику функции в точке х=2

    y`(2)=2*2-3=4-3=1  k2=1

    y(2)=2^2-3*2+2=4-6+2=0

    y=0+1(x-2)=x-2 -уравнение касательной в точке х=2

4) Коэффициент угла наклона первой касательной k1=-1, а второй касательной k2=1,

    следовательно, касательные взаимно перпендикулярны,

    т.е.угол между ними равен 90 градусов.

Выполнив деление получим:

Введём замену. Пусть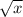 = t ≥ 0, тогда x = .

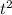Перепишем данное выражение с учётом замены. Получим:

 Найдём корни всех квадратных трёхчленов в числителе и разложим их на множители:

Разложение будет иметь вид:  2(t + 2)(t - 0.5)

Аналогично поступаем со вторым:

Разложение имеет вид: -2(t - 3)(t + 0.5)

Подставим вместо трёхчленов их разложения и проведём некторые преобразования, но оговоримся, что поскольку преобразование идёт лишь при допустимых значениях переменных, то t≥0; t≠3:

\\ = 4t^{2} - 1 - 4t{2} = -1