из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
a = 563/51
Объяснение:
|9x + 7a - 3| = |4x + 3a + 4|
Здесь не нужна никакая разность квадратов.
Возможно всего два варианта:
1) 9x + 7a - 3 = -4x - 3a - 4
13x + 10a + 1 = 0
x1 = (-10a - 1)/13
2) 9x + 7a - 3 = 4x + 3a + 4
5x + 4a - 7 = 0
x2 = (-4a + 7)/5
Нам надо, чтобы эти корни были разными. Найдем, при каком а они одинаковы.
(-10a - 1)/13 = (-4a + 7)/5
5(-10a - 1) = 13(-4a + 7)
-50a - 5 = -52a + 91
-50a + 52a = 91 + 5
2a = 96
a = 48
Значит, а не должно быть равно 48.
И нам надо, чтобы среднее арифметическое этих корней было -8.
(x1 + x2)/2 = -8
x1 + x2 = -16
(-10a - 1)/13 + (-4a + 7)/5 = -16
5(-10a - 1) + 13(-4a + 7) = -16*13*5
-50a - 5 - 52a + 91 = -1040
-102a = -1040 + 5 - 91 = -1126
a = -1126/(-102) = 1126/102 = 563/51
Оно не равно 48, значит, это решение.
Объяснение:
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
у = cos(x) вдоль оси оx на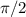 единиц влево
единиц влево
ну и вот что должно получиться.