Войти Регистрация Спроси ai-bota

По условии задачи составьте выражение с переменным. в первой вазе стояло x роз, а во второй - y роз. затем из перовой вазы взяли 2 розы, а во вторую поставили еще 5 роз. сколько роз стало в обеих ваз вместе?

Показать ответ

Ответ:

0005zet

27.12.2020 20:48

32

Объяснение:

154 ребёнка планировалось

154+6=160 (детей) поехало

Пусть планировалось х автобусов. Тогда приехало (х-2) автобуса. Планировалось посадить по (154/х) детей в каждый автобус. Посадили по (160/ (х-2)). Т.к. посадили в каждый автобус на 10 человек больше, чем они рассчитывали, то составим и решим уравнение

160/(х-2) - 154/х=10

Умножим на х *(х-2)

160х-154(х-2) =10 х(х-2)

10х²-20х=160х-154х+308

10х²-26х-308=0

D= 26²+40*308= 676+12320=12996

х₁= (26+√12996)/20=(26+114)/20= 140/20=7

х₂ =(26-√12996)/20=(26-114)/20 < 0 (не подходит)

Планировалось 7 автобусов

154/7=22 (рб) планировалось в кажд. авт.

22+10 =32 (рб) оказалось в каждом.

Или 160/ (7-2) = 32

0,0(0 оценок)

Ответ:

ilyadmitriev0

10.08.2022 05:44

$(\frac{13}{3} )^{\frac{x^{2}+ x-3}{x+1} }\leq \frac{2}{3}* (6,5)^{x-\frac{3}{x+1} }$

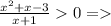ОДЗ: $\frac{x^{2}+ x-3}{x+1} 0=$ [-2,3; -1)∪[1,3; +∞)

$(\frac{13}{3} )^{\frac{x^{2}+ x-3}{x+1} }\leq \frac{2}{3}* (\frac{13}{2} )^{\frac{x^{2} +x-3}{x+1} }$

$(\frac{13}{3} )^{\frac{x^{2}+ x-3}{x+1} }: (\frac{13}{2} )^{\frac{x^{2} +x-3}{x+1} } \leq \frac{2}{3}$

$(\frac{13}{3}:\frac{13}{2} )^{\frac{x^{2}+ x-3}{x+1} } \leq \frac{2}{3}$

$(\frac{13}{3}*\frac{2}{13} )^{\frac{x^{2}+ x-3}{x+1} } \leq \frac{2}{3}$

$(\frac{2}{3})^{\frac{x^{2}+ x-3}{x+1} } \leq \frac{2}{3}$

$(\frac{2}{3})^{\frac{x^{2}+ x-3}{x+1} } \leq (\frac{2}{3})^1$

Так как основание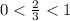 $0 < \frac{2}{3} < 1$ , то для показателей степеней справедливо неравенство:

${\frac{x^{2}+ x-3}{x+1} } \geq 1$

${\frac{x^{2}+ x-3}{x+1} } -1\geq 0$

${\frac{x^{2}+ x-3-x-1}{x+1} } \geq 0$

${\frac{x^{2}-4}{x+1} } \geq 0$

${\frac{(x-2)(x+2)}{x+1} } \geq 0$

- + - +

-2 -1 2

$-2\leq x < -1$ $x\geq 2$

[-2; -1) и [2; +∞)

удовлетворяет ОДЗ

ответ: [-2; -1)∪[2; +∞)

0,0(0 оценок)

Популярные вопросы: Алгебра

slarina171

12.01.2022 22:38

Выражение (1-2ab/(a^2+b^2))*(a^2+ b^2)...

ramil161

21.10.2020 15:00

Решите логарифмическое неравенство: log 1/9^x+log(3)^9x 3...

Telman07

21.10.2020 15:00

Докажите тождество: 1+tg^2a/1+ctg^2a=tg^2a...

buschckovaanas

26.06.2021 10:30

Запиши одночлены в стандартном виде и укажи те, у которых одинаковая буквенная часть. 1)3p5⋅6k2)k6p2⋅9k3p123)12k14⋅2p94)5pk⋅7,8k65)6k9p14⋅7,8 Одночлены в стандартном...

Darya0012

24.10.2021 20:33

1.Задача на готовом чертеже. Требуется найти ВО, если ОD=10. (Нужно только решение) 2. Если две стороны и угол между ними одного треугольника соответственно равны двум...

mujgan04

03.06.2020 19:53

1).раскройте скобки a-(3b+2c) 2)x+(-3m+2x) 3)-(b+no)+(-4a+c) 4)(x+3)-(8-x)+(10-x)...

DeNiSNoNs

09.12.2022 08:46

ответ 24 X 4.6е Проверенный ответлинейная функция- функция, графиккоторой является прямой линией, счем и связано ее название.у=kx+b это формула линейнойфункцииСоня11....

galeevaazaliyaqwert

15.08.2020 00:53

По графику найдите значение y, если x = -4....

kopiplay

19.08.2022 20:30

Дано: О=ОС,АО=ОС доказать что Д равен Б срчоно...

Милааа11

27.02.2020 16:38

Найди корни уравнения s3−121s/12=0. s1= s2= s3= корни вводи по возрастанию, первым — наименьший...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку